 Problem C. 1197. (December 2013)
Problem C. 1197. (December 2013)
C. 1197. Point E lies on side AD of a square ABCD of area 64 units. Point F lies on the extension of side AB beyond vertex B. These two points and vertex C form an isosceles right-angled triangle of area 50 units. What is the area of triangle AFE?
(5 pont)
Deadline expired on January 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
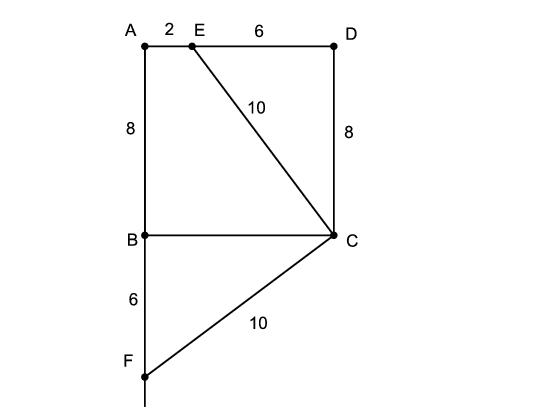
Megoldás. A négyzet oldala 8 egység. Mivel \(\displaystyle ECF\) területe 50, így \(\displaystyle EC\cdot FC=100\). Mivel a két tényező egyenlő, ezért \(\displaystyle EC = FC = 10\). Pitagorasz-tétellel \(\displaystyle ED = 6\), vagyis \(\displaystyle EA = 2\). A megadott derékszögek miatt \(\displaystyle DCE\angle=BCF\angle\), így a \(\displaystyle DCE\) háromszög és a \(\displaystyle BCF\) háromszög egybevágó. Ezért \(\displaystyle BF = 6\). Az \(\displaystyle AFE\) háromszög derékszögű, befogóinak hossza: \(\displaystyle EA = 2\), \(\displaystyle AF = AB + BF = 14\), így a területe 14.
Statistics:
166 students sent a solution. 5 points: 143 students. 4 points: 14 students. 3 points: 6 students. 1 point: 1 student. 0 point: 1 student. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, December 2013
