 Problem C. 1204. (January 2014)
Problem C. 1204. (January 2014)
C. 1204. The midpoints of the sides of the convex quadrilaterals ABCD and EFGH coincide. Prove that the two quadrilaterals have equal areas.
(5 pont)
Deadline expired on February 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Bebizonyítjuk, hogy tetszőleges konvex négyszög területe kétszerese a felezőpontjai által meghatározott négyszög területének. Ebből már következik az állítás, hiszen ha két négyszög oldalfelezőpontjai egybeesnek, akkor az általuk meghatározott négyszög is egybeesik, így ezek területe nyilván ugyanakkora, és így az eredeti négyszögek területe is egyenlő.
Tekintsük a következő ábrát.
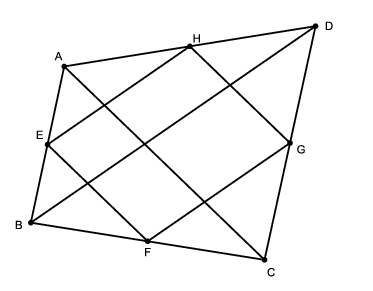
Mivel E és F felezőpontok, ezért a B középpontú, 1:2 arányú kicsinyítés az ABC háromszöget az EBF háromszögbe viszi: , a hasonlóság aránya 1:2. A területek aránya ennek négyzete, tehát
.
Hasonlóan kapjuk, hogy ,
és
.
Ezeket összeadva:
Ebből pedig már következik az állítás:
Statistics:
93 students sent a solution. 5 points: 65 students. 4 points: 13 students. 3 points: 4 students. 2 points: 2 students. 1 point: 5 students. 0 point: 3 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, January 2014
