 |
A C. 1208. feladat (2014. január) |
C. 1208. Adottak a síkon a PQRL és az LSTA azonos körüljárású paralelogrammák, melyeknek az L ponton kívül nincs közös része. Igazoljuk, hogy mindig található egy (esetleg hurkolt vagy elfajuló) ABCDE ötszög a síkon, amelyben az oldalak felezőpontjai a megadott sorrendben P, Q, R, S, T.
(5 pont)
A beküldési határidő 2014. február 10-én LEJÁRT.
Megoldás. A bizonyításhoz kihasználjuk a vektorokra vonatkozó paralelogramma szabályt, amely miatt \(\displaystyle \overrightarrow{LQ}=\overrightarrow{LP}+\overrightarrow{LR}\), illetve \(\displaystyle \overrightarrow{LT}=\overrightarrow{LA}+\overrightarrow{LS}\).
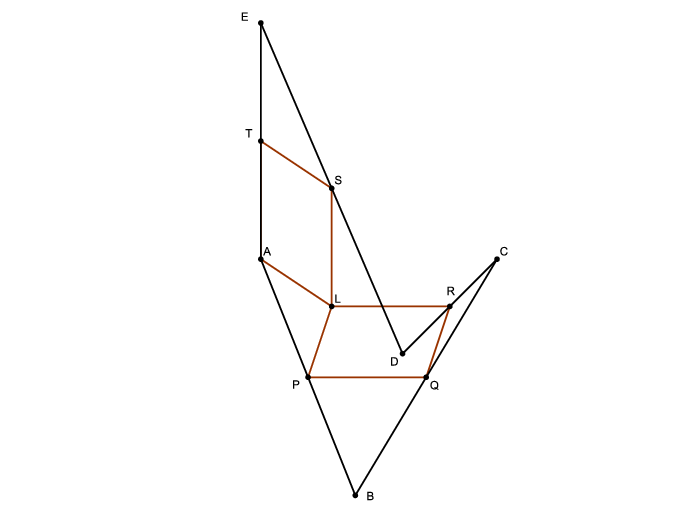
Felhasználjuk még, hogy az \(\displaystyle \overrightarrow{a}\) és \(\displaystyle \overrightarrow{b}\) vektor felezőpontjába mutató \(\displaystyle \overrightarrow{v}\) vektorra \(\displaystyle \overrightarrow{v}=\frac{\overrightarrow{a}+\overrightarrow{b}}{2}\), amiből \(\displaystyle \overrightarrow{b}=2\overrightarrow{v}-\overrightarrow{a}\).
Azt fogjuk bizonyítani, hogy az \(\displaystyle A\) pontot sorra tükrözve a \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\), \(\displaystyle S\) és \(\displaystyle T\) pontokra, az utolsó tükörkép maga az \(\displaystyle A\) pont lesz.
Jelölje tehát az \(\displaystyle A\) pont tükörképét a \(\displaystyle P\) pontra \(\displaystyle B\). Ekkor \(\displaystyle \overrightarrow{LB}=2\overrightarrow{LP}-\overrightarrow{LA}.\)
A \(\displaystyle B\) pont tükörképe a \(\displaystyle Q\) pontra legyen \(\displaystyle C\). Ekkor \(\displaystyle \overrightarrow{LC}=2\overrightarrow{LQ}-\overrightarrow{LB}= 2(\overrightarrow{LP}+\overrightarrow{LR})-(2\overrightarrow{LP}-\overrightarrow{LA}) =2\overrightarrow{LR}+\overrightarrow{LA}\).
A \(\displaystyle C\) pont tükörképe az \(\displaystyle R\) pontra legyen \(\displaystyle D\). Ekkor \(\displaystyle \overrightarrow{LD}=2\overrightarrow{LR}-\overrightarrow{LC}= 2\overrightarrow{LR}-(2\overrightarrow{LR}+\overrightarrow{LA})=-\overrightarrow{LA}\).
A \(\displaystyle D\) pont tükörképe az \(\displaystyle S\) pontra legyen \(\displaystyle E\). Ekkor \(\displaystyle \overrightarrow{LE}=2\overrightarrow{LS}-\overrightarrow{LD}=2\overrightarrow{LS}+\overrightarrow{LA}\).
Végül az \(\displaystyle E\) pont tükörképét a \(\displaystyle T\) pontra jelölje \(\displaystyle F\). Ekkor \(\displaystyle \overrightarrow{LF}=2\overrightarrow{LT}-\overrightarrow{LE}= 2(\overrightarrow{LA}+\overrightarrow{LS})-(2\overrightarrow{LS}+\overrightarrow{LA})=\overrightarrow{LA}\).
Vagyis \(\displaystyle \overrightarrow{LF}=\overrightarrow{LA}\), és így valóban \(\displaystyle F\equiv A\), tehát az így kapott \(\displaystyle ABCDE\) ötszög megfelelő.
Statisztika:
20 dolgozat érkezett. 5 pontot kapott: Bereczki Zoltán, Farkas Dóra, Fényes Balázs, Gnandt Balázs, Hegel Patrik, Jójárt Alexandra, Telek Máté László. 4 pontot kapott: Chourfi Abdel Karim, Demeter Dániel, Hegyesi János Géza, Szabó 524 Tímea, Temesvári Fanni. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2014. januári matematika feladatai

