 Problem C. 1209. (January 2014)
Problem C. 1209. (January 2014)
C. 1209. The tangents drawn from a point C lying outside a circle touch the circle at points A és B. M is a point on the shorter arc AB. Let MN, ME and MD be the line segments drawn from M, perpendicular to the line segments AB, BC and CA, respectively. Given that MN=4, MD=2 and , find the area of triangle MNE.
(5 pont)
Deadline expired on February 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Készítsünk ábrát.
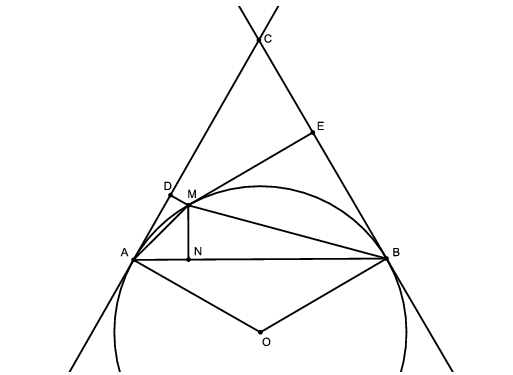
A kerületi szögek tétele miatt DAM =MBA
=MBA , mindkettő az MA ívhez tartozó kerületi szög; illetve EBM
, mindkettő az MA ívhez tartozó kerületi szög; illetve EBM =MAB
=MAB , hiszen mindkettő az MB ívhez tartozó kerületi szög. Tudjuk még, hogy MDA
, hiszen mindkettő az MB ívhez tartozó kerületi szög. Tudjuk még, hogy MDA =MNB
=MNB =90o és MEB
=90o és MEB =MNA
=MNA =90o. Ezekből már - két-két szög egyenlősége miatt - következik, hogy
=90o. Ezekből már - két-két szög egyenlősége miatt - következik, hogy és
. Mivel DM=2 és MN=4, ezért a DAM és az NBM háromszög esetén a hasonlóság aránya 1:2, és így MB=2MA. Ebből pedig az következik, hogy az EBM és az NAM háromszög esetén a hasonlósági arány 2:1. Innen pedig EM=2MN=8 következik.
Az EBM és az NAM háromszög hasonlóságából az is következik, hogy EMB =AMN
=AMN . Emiatt NME
. Emiatt NME =NMB
=NMB +EMB
+EMB =NMB
=NMB +AMN
+AMN =120o.
=120o.
Az MNE háromszög területe: .
Statistics:
30 students sent a solution. 5 points: Barna Kinga, Beke 997 Tamás, Bekő Mária, Bereczki Zoltán, Chourfi Abdel Karim, Demeter Dániel, Denke Dorottya, Farkas Dóra, Gnandt Balázs, Hegel Patrik, Hegyesi János Géza, Hegyi Zoltán, Kácsor Szabolcs, Kovács 972 Márton, Kranczler Dóra, Paulovics Zoltán, Rimóczi Alma, Sziegl Benedek, Telek Máté László, Temesvári Fanni, Tóth Zsófia, Zsiros Ádám. 4 points: Szabó 157 Dániel. 3 points: 2 students. 2 points: 2 students. 1 point: 1 student. 0 point: 2 students.
Problems in Mathematics of KöMaL, January 2014
