 Problem C. 1215. (February 2014)
Problem C. 1215. (February 2014)
C. 1215. Prove that if the inscribed circle of a right-angled triangle has unit radius and the length of one leg is rational then the lengths of the other two sides are also rational.
(5 pont)
Deadline expired on March 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Készítsünk ábrát. Az \(\displaystyle ABC\) háromszögbe írható kör középpontja legyen \(\displaystyle O\), az oldalak szokás szerint \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), az érintési pontok pedig \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\). Mivel egy kör középpontjából húzott sugár merőleges az érintőre, így egyrészt \(\displaystyle OE=OD=1\), másrészt \(\displaystyle ODC\angle=OEC\angle=90^{\circ}\). Mivel \(\displaystyle DCE\angle\) is derékszög, így \(\displaystyle CEOD\) olyan téglalap, melynek szomszédos oldalai egyenlők, tehát négyzet. Így \(\displaystyle CE=CD=1\), amiből \(\displaystyle EA=b-1\) és \(\displaystyle DB=a-1\) következik. Mivel külső pontból egy körhöz húzott érintőszakaszok egyenlő hosszúak, ezért \(\displaystyle FA=EA=b-1\) és \(\displaystyle FB=DB=a-1\).
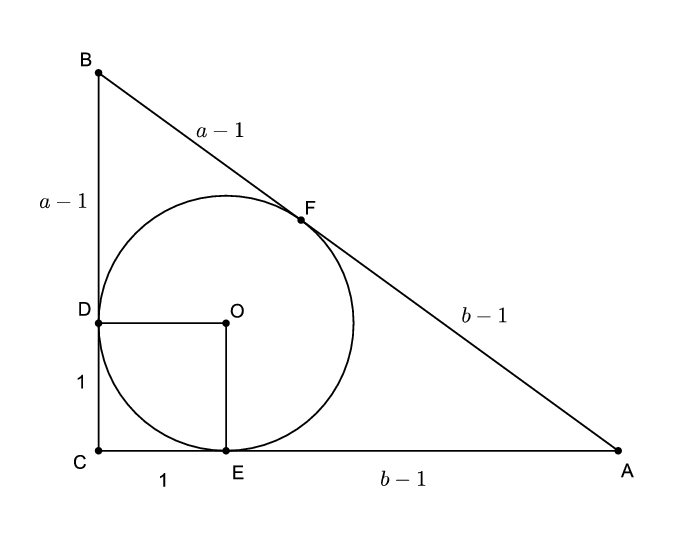
Legyen az \(\displaystyle a\) racionális (ezt szimmetria okokból feltehetjük). Mivel \(\displaystyle c=a-1+b-1\), amiből \(\displaystyle c-b=a-2\), és ha \(\displaystyle a\) racionális, akkor \(\displaystyle a-2\) is az, ezért \(\displaystyle c-b\) is racionális. Felírva a Pitagorasz tételt: \(\displaystyle a^2+b^2=c^2\), amiből \(\displaystyle a^2=c^2-b^2=(c+b)(c-b)\). Mivel \(\displaystyle c>b\), ezért ebből \(\displaystyle c+b=\frac{a^2}{c-b}\) következik. Mivel \(\displaystyle a\) racionális, ezért \(\displaystyle a^2\) is az, és mivel \(\displaystyle c-b\) is az, így a kettő hányadosa, \(\displaystyle c+b\) is az. Mivel \(\displaystyle c=\frac{(c-b)+(c+b)}{2}\), ahol a nevezőben két racionális szám összege áll, így \(\displaystyle c\) is racionális. Végül \(\displaystyle b=c-(c-b)\) miatt \(\displaystyle b\) két racionális szám összege, így maga is racionális.
Statistics:
43 students sent a solution. 5 points: Bajnok Anna, Bálint Karola, Bekő Mária, Bereczki Zoltán, Demeter Dániel, Denke Dorottya, Dombrovszky Borbála, Erdei Ákos, Fényes Balázs, Fülöp Erik, Gnandt Balázs, Hegel Patrik, Hegyi Zoltán, Horváth Bendegúz, Jójárt Alexandra, Kácsor Szabolcs, Kovács 972 Márton, Kranczler Dóra, Krisztián Jonatán, Nguyen Anh Tuan, Porupsánszki István, Rimóczi Alma, Schefler Barna, Semegi Judit, Szabó 157 Dániel, Sziegl Benedek, Szűcs Dorina, Szűcs Miklós, Tarnay Mátyás, Tekeli Miklós, Temesvári Fanni, Tóth Zsófia, Várkonyi Ádám, Wolkensdorfer Zsófia, Zsiros Ádám. 4 points: Chourfi Abdel Karim. 3 points: 3 students. 2 points: 2 students. 1 point: 2 students.
Problems in Mathematics of KöMaL, February 2014
