 Problem C. 1216. (February 2014)
Problem C. 1216. (February 2014)
C. 1216. The ideal carnival doughnut weighs 54 grams when done, and 8% is the oil absorbed during frying. It is shaped like a (centrally symmetrical) spherical segment of diameter 78 mm and height 3 cm. The volume of the dough is doubled in frying, and its mass is only increased by the oil absorbed. Before frying, the whole dough weighs 1 kg, and it is kept in a 2.5-litre bowl. Is it possible to cover the bowl with a flat lid?
(5 pont)
Deadline expired on March 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Egy fánk 54 gramm, ebből \(\displaystyle 54\cdot0,92=49,68\) gramm a tészta.
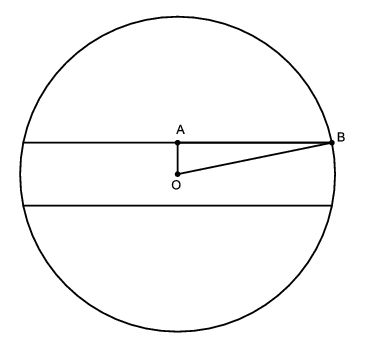
A gömböv átmérője 78 mm= 7,8 cm, vagyis \(\displaystyle OB=7,8/2=3,9\) cm. A fánk magassága az \(\displaystyle AO\) hosszának kétszerese, vagyis \(\displaystyle AO=1,5\) cm. \(\displaystyle AB\) Pitagorasz tétellel számolható: \(\displaystyle AB=\sqrt{3,9^2-1,5^2}=3,6\) cm. Egy kisütött fánk térfogata így: \(\displaystyle V=2\cdot\frac{\pi}{6}\cdot1,5\cdot(1,5^2+3\cdot3,9^2+3\cdot3,6^2)\approx136,28 {\rm ~cm}^3\). A sütés előtti térfogat ennek a fele, vagyis kb. 68,14 \(\displaystyle {\rm cm}^3\).
Tehát 49,68 gramm tészta térfogata 68,14 \(\displaystyle {\rm cm}^3\), így 1000 gramm tészta térfogata \(\displaystyle \frac{68,14}{49,68}\cdot1000\approx1371,58 {\rm~ cm}^3 < 2500 {\rm~ cm}^3\), azaz bőven belefér a tálba.
Statistics:
43 students sent a solution. 5 points: Bálint Karola, Bereczki Zoltán, Chourfi Abdel Karim, Denke Dorottya, Farkas Dóra, Fényes Balázs, Fülöp Erik, Hegel Patrik, Jójárt Alexandra, Kranczler Dóra, Krisztián Jonatán, Sebők Bence, Semegi Judit, Szabó 145 Bernát, Szabó 157 Dániel, Tekeli Miklós, Telek Máté László, Temesvári Fanni, Torma Lili Eszter, Tóth Zsófia. 4 points: Beke 997 Tamás, Demeter Dániel, Kovács 972 Márton, Nguyen Anh Tuan. 3 points: 13 students. 2 points: 6 students.
Problems in Mathematics of KöMaL, February 2014
