Problem C. 1218. (March 2014)

C. 1218. On a circular table of radius 80 cm, the square tablecloth has been pulled aside, such that one corner lies exactly on the edge of the table, and the two sides that meet at the opposite vertex are tangent to the edge of the table. Determine the length of the side of the tablecloth to the nearest millimetre.

(5 pont)

Deadline expired on April 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

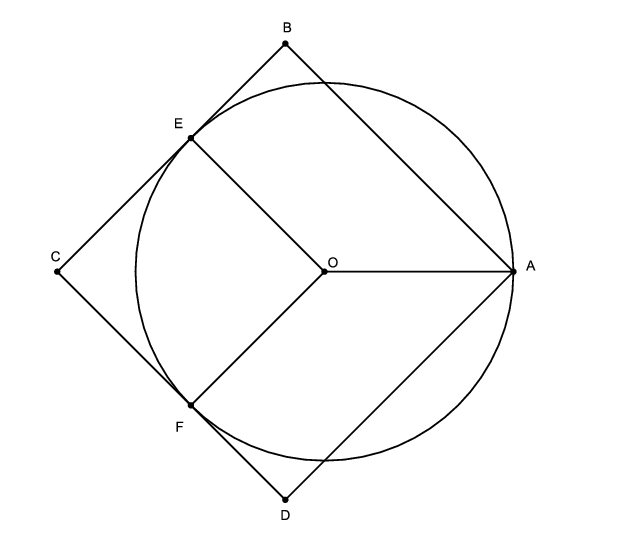
Megoldás. A terítő négy sarkát jelölje \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\), az illeszkedő csúcs legyen az \(\displaystyle A\), a \(\displaystyle BC\) a kört érintse \(\displaystyle E\)-ben, a \(\displaystyle DC\) pedig \(\displaystyle F\)-ben, a kör középpontját pedig jelölje \(\displaystyle O\). Mivel egy érintő merőleges az érintési pontba húzott sugárra, ezért az \(\displaystyle OECF\) négyszög \(\displaystyle E\), \(\displaystyle C\) és \(\displaystyle F\) csúcsánál derékszög van, valamint \(\displaystyle OE=OF=r\), tehát a négyszög négyzet. Így az \(\displaystyle OEC\) háromszög egyenlőszárú, a szárak hossza \(\displaystyle r\), ezért \(\displaystyle OC=r\sqrt2\). A szimmetria miatt \(\displaystyle C\), \(\displaystyle O\) és \(\displaystyle A\) egy egyenesen vannak, tehát \(\displaystyle AC=r+r\sqrt2\). Mivel \(\displaystyle AB=\frac{AC}{\sqrt2}\), ezért \(\displaystyle AB=\frac{r+r\sqrt2}{\sqrt2}=\frac{r}{\sqrt2}+r=\frac{80}{\sqrt2}+80\approx136,6~{\rm (cm)}\).

Statistics:

104 students sent a solution.
5 points:	Brányi Balázs, Horváth 016 Gábor, Kardos Bálint Tamás, Knoch Júlia, Kocsis Júlia, Kovács 246 Benedek, Papp 535 Ágnes, Polgár Márton, Radnai Bálint, Révy Gábor, Szécsi Adél Lilla, Széles Katalin, Szemerédi Levente, Zsakó Ágnes.
4 points:	Bodonhelyi Anna, Bottlik Judit, Döbröntei Dávid Bence, Ghyczy András, Györök Lídia, Hegedűs Henrietta, Kerekes Anna, Kis 913 Levente, Klász Viktória, Kovács 526 Tamás, Kovács Kristóf, Kovács Péter Tamás, Molnár-Sáska Zoltán, Pap-Takács Mónika, Ratkovics Gábor, Sándor Gergely, Schefler Barna, Szűcs 324 Ágnes, Vágó Richárd.
3 points:	15 students.
2 points:	20 students.
1 point:	28 students.
0 point:	8 students.

Problems in Mathematics of KöMaL, March 2014