 Problem C. 1221. (March 2014)
Problem C. 1221. (March 2014)
C. 1221. F is the midpoint of side AD of a square ABCD. N is the point lying closer to B that divides side AB in a 1:3 ratio. In what ratio does the circumscribed circle of triangle AFN divide the diagonal AC?
(5 pont)
Deadline expired on April 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyenek a négyzet csúcsainak koordinátái \(\displaystyle A(0;0)\), \(\displaystyle B(4;0)\), \(\displaystyle C(4,4)\) és \(\displaystyle D(0,4)\). Ekkor \(\displaystyle F(0;2)\) és \(\displaystyle N(3;0)\).
Az \(\displaystyle AFN\) háromszög derékszögű, körülírt körének középpontja az \(\displaystyle FN\) szakasz felezőpontja, \(\displaystyle K(1,5;1)\). A kör sugara \(\displaystyle r=\frac{FN}{2}=\frac{\sqrt{(-3)^2+2^2}}{2}=\frac{\sqrt{13}}{2}\). Így a kör egyenlete: \(\displaystyle (x-1,5)^2+(y-1)^2=\frac{13}{4}\).
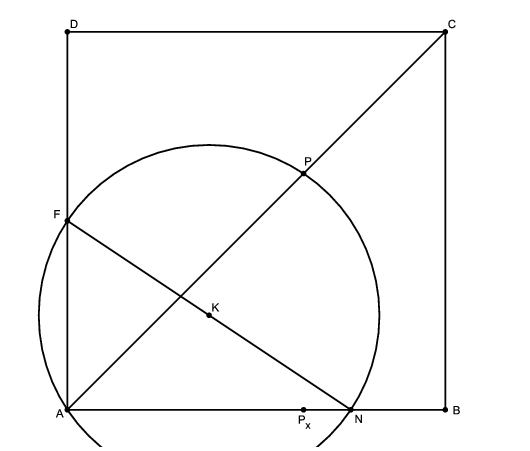
Az \(\displaystyle AC\) átló egyenesének egyenlete \(\displaystyle x=y\). Ezt behelyettesítve a kör egyenletbe, majd az egyenletet rendezve és megoldva:
\(\displaystyle (x-1,5)^2+(x-1)^2=\frac{13}{4},\)
\(\displaystyle x^2-3x+2,25+x^2-2x+1=3,25,\)
\(\displaystyle 2x^2-5x=0,\)
\(\displaystyle x(2x-5)=0,\)
\(\displaystyle x_1=0\) és \(\displaystyle x_2=2,5\).
Tehát a két metszéspont \(\displaystyle A(0;0)\) és \(\displaystyle P(2,5;2,5)\).
Legyen \(\displaystyle P_x(\frac52;0)\). Ekkor a párhuzamos szelők tétele szerint \(\displaystyle \frac{AP}{PC}=\frac{AP_x}{P_xB}=\frac{2,5}{1,5}=\frac53\), tehát az \(\displaystyle AFN\) háromszög köré írt köre az \(\displaystyle AC\) átlót 5:3 arányban osztja .
Statistics:
113 students sent a solution. 5 points: 53 students. 4 points: 36 students. 3 points: 9 students. 2 points: 6 students. 1 point: 6 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, March 2014
