 Problem C. 1224. (April 2014)
Problem C. 1224. (April 2014)
C. 1224. The integer that consists of \(\displaystyle m\) digits of 9 and the integer that consists of \(\displaystyle n\) digits of 9 are multiplied together. What is the sum of the digits of the product?
(5 pont)
Deadline expired on May 12, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Ha \(\displaystyle m=n\), akkor a két szám szorzata \(\displaystyle (10^m-1)(10^m-1)=10^{2m}-2\cdot10^m+1\).
A \(\displaystyle 10^{2m}\) szám végén \(\displaystyle 2m\) darab 0 áll, a \(\displaystyle 2\cdot10^m\) végén pedig \(\displaystyle m\) darab, így kivonva őket egymásból:
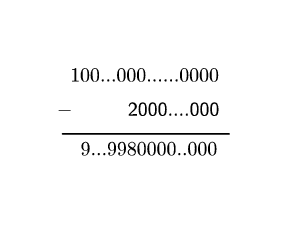
A különbségben elöl \(\displaystyle m-1\) darab 9-es áll, utána egy 8-as, a végén pedig \(\displaystyle m\) darab 0, így ehhez még 1-et adva a számjegyek összege \(\displaystyle 9(m-1)+8+1=9m\).
Ha \(\displaystyle m\neq n\), akkor legyen pl. \(\displaystyle m<n\). Ekkor \(\displaystyle (10^m-1)(10^n-1)=10^{m+n}-10^m-10^n+1\).
Ekkor tekintsük azt a kivonást, melyben \(\displaystyle 10^{m+n}\)-ből kivonjuk \(\displaystyle 10^m+10^n\)-t. Ez utóbbi szám úgy néz ki, hogy a szám végén áll \(\displaystyle m\) darab 0, előtte egy 1-es, azelőtt pedig \(\displaystyle n-1-m\) darab 0, és a szám elején megint 1-es. \(\displaystyle 10^{m+n}\) pedig gy 1-es és utána \(\displaystyle m+n\) darab 0. Ezek különbsége:

A szám végén áll \(\displaystyle m\) darab 0, előtte \(\displaystyle n-m\) darab 9-es, azelőtt egy 8-as, azelőtt pedig \(\displaystyle m+n-1-n=m-1\) darab 9-es számjegy. Ehhez 1-et hozzáadva a számjegyek összege \(\displaystyle 9\cdot(m-1+n-m)+8+1=9n\).
Statistics:
86 students sent a solution. 5 points: Balázs Ákos Miklós, Borbényi Márton, Brányi Balázs, Döbröntei Dávid Bence, Erdődi Ádám Károly, Gáspár Attila, Horváth 016 Gábor, Kerekes Anna, Kis 913 Levente, Klász Viktória, Kovács 526 Tamás, Mándoki László, Mihálykó Péter, Molnár-Sáska Zoltán, Novák Márk, Papp 535 Ágnes, Polgár Márton, Radnai Bálint, Sándor Gergely, Solti Emese, Somogyi Pál, Szécsi Adél Lilla, Török Réka , Uzonyi 000 Ákos, Varsányi András, Zsakó Ágnes. 4 points: Árvai Balázs, Bereczki Ádám, Jób Csongor, Knoch Júlia, Kocsis Júlia, Kormányos Hanna Rebeka, Kovács 162 Viktória, Kovács Péter Tamás, Marticsek Réka, Matusek Márton, Pap-Takács Mónika, Sebastian Fodor, Szécsényi Nándor, Széles Katalin, Szücs Patrícia, Vass Máté. 3 points: 17 students. 2 points: 11 students. 1 point: 5 students. 0 point: 6 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, April 2014
