Problem C. 1227. (April 2014)

C. 1227. The lengths of the bases of a trapezium are 7 and 1. The trapezium is divided into two parts of equal area with a line parallel to the bases. Find the length of the segment of this parallel line that lies inside the trapezium.

(5 pont)

Deadline expired on May 12, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen az \(\displaystyle ABCD\) trapézban \(\displaystyle CD=1\), \(\displaystyle AB=7\), a keresett egyenesnek a trapézba eső szakasza \(\displaystyle MN\), hossza \(\displaystyle x\). Az \(\displaystyle AD\) és \(\displaystyle BC\) egyenes metszéspontját jelölje \(\displaystyle O\). Az \(\displaystyle ODC\), az \(\displaystyle OMN\) és az \(\displaystyle OAB\) háromszög magassága legyen rendre \(\displaystyle m\), \(\displaystyle m_1\) és \(\displaystyle m_2\).

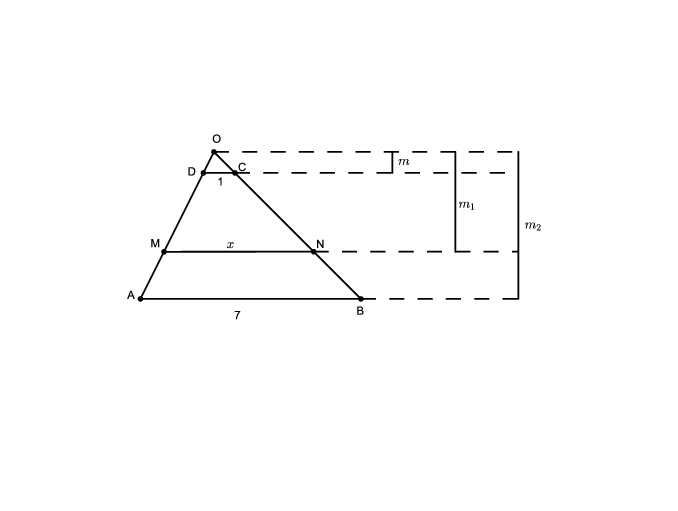
\(\displaystyle DC||MN\), így az \(\displaystyle ODC\) és az \(\displaystyle OMN\) háromszögek hasonlók, így megfelelő szakaszaik aránya megegyezik: \(\displaystyle \frac 1x=\frac{m}{m_1}\), amiből \(\displaystyle m_1=mx\).

Ugyanígy az \(\displaystyle ODC\) és az \(\displaystyle OAB\) háromszögek is hasonlóak, és így \(\displaystyle \frac17=\frac{m}{m_2}\), amiből \(\displaystyle m_2=7m\).

A \(\displaystyle DMNC\) trapéz magassága \(\displaystyle m_1-m=mx-m=m(x-1)\), míg az \(\displaystyle ABCD\) trapéz magassága \(\displaystyle m_2-m=7m-m=6m\). Az előbbi területe fele az utóbbinak:

\(\displaystyle 2\cdot\frac{(1+x)m(x-1)}{2}=\frac{(1+7)\cdot6m}{2},\)

\(\displaystyle m>0\)-val osztva és rendezve:

\(\displaystyle (1+x)(x-1)=24,\)

\(\displaystyle x^2=25,\)

és innen \(\displaystyle x>0\) miatt \(\displaystyle x=5\) következik.

Statistics:

114 students sent a solution.
5 points:	100 students.
4 points:	4 students.
3 points:	8 students.
2 points:	2 students.

Problems in Mathematics of KöMaL, April 2014