 Problem C. 1230. (April 2014)
Problem C. 1230. (April 2014)
C. 1230. Three lattice points are selected at random out of the lattice points lying on the circle of equation \(\displaystyle x^2+y^2-2x-4y-45=0\). What is the probability that the three points form a right-angled triangle?
(5 pont)
Deadline expired on May 12, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás.
\(\displaystyle x^2+y^2-2x-4y-45=(x-1)^2+(y-2)^2-5-45=0,\)
\(\displaystyle (x-1)^2+(y-2)^2=50,\)
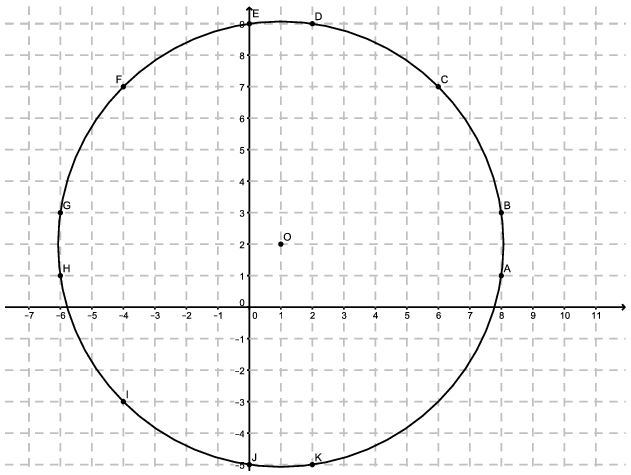
tehát a kör középpontja a \(\displaystyle O(1;2)\), a sugara \(\displaystyle r=\sqrt{50}\). Összesen 12 rácspont van a körvonalon. Ezek 6 átmérőt határoznak meg. Minden átmérőhöz a további 10 pont bármelyikét hozzávehetjük, ekkor derékszögű háromszöget kapunk, és csak így kapunk derékszögű háromszöget. Vagyis \(\displaystyle 6\cdot10=60\) esetben kapunk derékszögű háromszöget. Összesen \(\displaystyle \binom{12}{3}=220\)-féleképp választhatunk ki három rácspontot. A keresett valószínűség tehát: \(\displaystyle \frac{60}{220}=\frac{3}{11}\).
Statistics:
31 students sent a solution. 5 points: Bálint Karola, Bekő Mária, Bereczki Zoltán, Denke Dorottya, Erdei Ákos, Fényes Balázs, Fülöp Erik, Hegyi Zoltán, Horváth Bendegúz, Jójárt Alexandra, Kranczler Dóra, Krisztián Jonatán, Molnár Dávid, Nagy Dávid, Nguyen Anh Tuan, Paulovics Zoltán, Porupsánszki István, Rimóczi Alma, Szabó 524 Tímea, Sziegl Benedek, Szűcs Dorina, Telek Máté László, Várkonyi Ádám. 4 points: Farkas Bence, Tari Balázs. 3 points: 5 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, April 2014
