Problem C. 1234. (May 2014)

C. 1234. One angle of a kite is a right angle, the measure of the opposite angle is \(\displaystyle 30^\circ\), and the length of the shorter side is 10 cm. Find the length of the side of the square that has a vertex on each of three sides of the kite, and has a side parallel to the longer side of the kite.

(5 pont)

Deadline expired on June 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Két eset van, az egyikben a három csúcsból kettő a rövidebbik oldalra esik, a másikban pedig a hosszabbik oldalra. Mindkét esetben jelölje a deltoid derékszögű csúcsát \(\displaystyle C\), a vele szemközti csúcsot \(\displaystyle A\). Mivel az \(\displaystyle A\) csúcsnál lévő szög \(\displaystyle 30^{\circ}\)-os, így a másik két szög \(\displaystyle 120^{\circ}\).

Az \(\displaystyle EFGH\) négyzet \(\displaystyle HE\) oldala párhuzamos \(\displaystyle BA\)-val, ezért \(\displaystyle HED\angle=BAE\angle\), mert párhuzamos szárú szögek. Így \(\displaystyle HED\angle=30^{\circ}\), és így a \(\displaystyle HDE\) háromszög harmadik szöge, \(\displaystyle DHE\angle=180^{\circ}-120^{\circ}-30^{\circ}=30^{\circ}\). Jelölje \(\displaystyle D\) merőleges vetületét \(\displaystyle HE\)-re \(\displaystyle D'\).

I. eset. Legyen \(\displaystyle EH=2x\). Ekkor a \(\displaystyle HDD'\) háromszög egy szabályos háromszög fele, melyben \(\displaystyle HD'=x\), és így \(\displaystyle HD=\frac{2}{\sqrt3}x\).

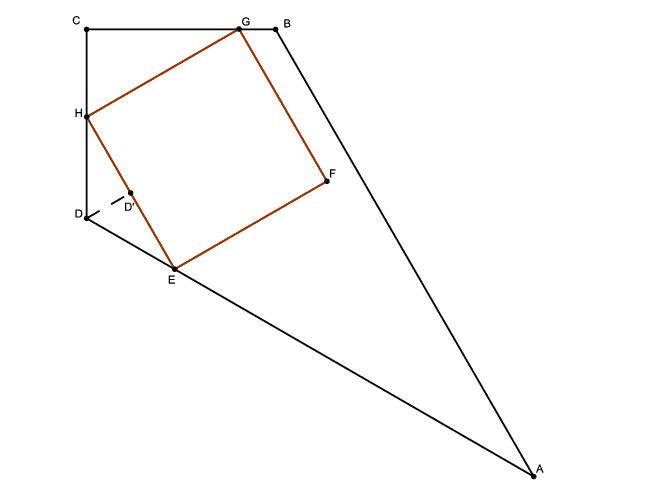
Tekintsük a \(\displaystyle HCG\) háromszöget. Itt \(\displaystyle HCG\angle=90^{\circ}\), \(\displaystyle CHG\angle=180^{\circ}-(DHE\angle+EHG\angle)=180^{\circ}-(30^{\circ}+90^{\circ})=60^{\circ}\), és így \(\displaystyle CGH\angle=30^{\circ}\), a \(\displaystyle HCG\) háromszög is egy szabályos háromszög fele. A háromszög oldala \(\displaystyle HG=2x\) és így \(\displaystyle HC=x\). Tudjuk, hogy \(\displaystyle DC=10\), ebből

\(\displaystyle 10=\frac{2}{\sqrt3}x+x=x\left(\frac{2}{\sqrt3}+1\right),\)

amiből a négyzet oldala már számolható:

\(\displaystyle 2x=\frac{20}{\frac{2}{\sqrt3}+1}=\frac{20\sqrt3}{2+\sqrt3}=\frac{20\sqrt3(2-\sqrt3)}{1}= 40\sqrt3-60\approx9,28~{\rm (cm)}.\)

II. eset. Legyen \(\displaystyle DH=x\). Ekkor a \(\displaystyle HDD'\) háromszög egy szabályos háromszög fele, melyben \(\displaystyle HD'=\frac{\sqrt3}{2}x\), és így a négyzet oldala \(\displaystyle \sqrt3x\). Mivel \(\displaystyle DC=10\), így \(\displaystyle HC=10-x\). Tekintsük a \(\displaystyle CHS\) háromszöget. Ebben az I. esetbeli \(\displaystyle HCG\) háromszögben látott módon \(\displaystyle CHS\angle=60^{\circ}\), a háromszög egy szabályos háromszög fele, így \(\displaystyle CS=\sqrt3(10-x)\) és \(\displaystyle HS=20-2x\). Az \(\displaystyle SGB\) háromszög szintén egy szabályos háromszög fele, hiszen a \(\displaystyle G\) csúcsnál derékszög van, az \(\displaystyle S\) csúcsnál pedig \(\displaystyle 30^{\circ}\). Mivel \(\displaystyle SG=\sqrt3x-(20-2x)\), így \(\displaystyle SB=\frac{2}{\sqrt3}(\sqrt3x-(20-2x))\).

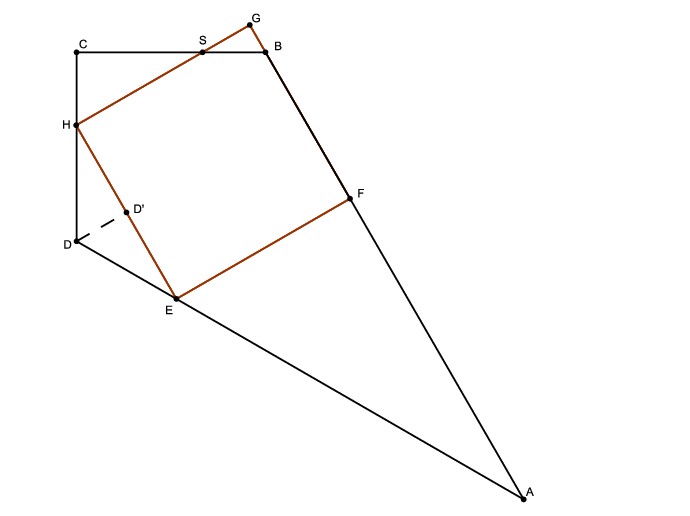
Mivel \(\displaystyle SB+CS=10\), így felírható a következő egyenlet, amiből majd \(\displaystyle \sqrt3x\)-et megkapjuk:

\(\displaystyle \frac{2}{\sqrt3}(\sqrt3x-(20-2x))+\sqrt3(10-x)=10,\)

\(\displaystyle 2x-\frac{40}{\sqrt3}+\frac{4}{\sqrt3}x+10\sqrt3-\sqrt3x=10,\)

\(\displaystyle 2\sqrt3x-40+4x+30-3x=10\sqrt3,\)

\(\displaystyle x(2\sqrt3+1)=10+10\sqrt3,\)

\(\displaystyle x=\frac{10+10\sqrt3}{2\sqrt3+1},\)

\(\displaystyle \sqrt3x=\frac{10\sqrt3+30}{2\sqrt3+1}=\frac{(10\sqrt3+30)(2\sqrt3-1)}{12-1}=\)

\(\displaystyle =\frac{60-10\sqrt3+60\sqrt3-30}{11}=\frac{30+50\sqrt3}{11}\approx 10,60~{\rm(cm)}.\)

Statistics:

72 students sent a solution.
5 points:	Bereczki Ádám, Bereczki Zoltán, Kerekes Anna, Kis 913 Levente, Papp 535 Ágnes, Széles Katalin, Sziegl Benedek.
4 points:	Polgár Márton.
3 points:	47 students.
2 points:	12 students.
1 point:	3 students.
0 point:	1 student.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, May 2014