Problem C. 1305. (September 2015)

C. 1305. A spiral is made out of a square of side \(\displaystyle n\) units, as shown in the figure, by always breaking the line 1 unit before reaching the already existing part of the spiral. Similarly, a spiral is made out of a regular triangle of side \(\displaystyle 1.8n\) units by breaking the line 1.8 units before closing up. (The diagram shows the two spirals for the case of \(\displaystyle n = 4\).) For what value of n will the lengths of the two spirals be equal?

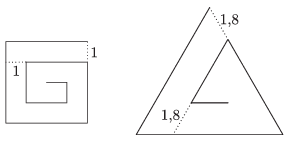
(5 pont)

Deadline expired on October 12, 2015.

Statistics:

250 students sent a solution.
5 points:	102 students.
4 points:	61 students.
3 points:	10 students.
2 points:	9 students.
1 point:	5 students.
0 point:	58 students.
Unfair, not evaluated:	5 solutionss.

Problems in Mathematics of KöMaL, September 2015