A C. 1317. feladat (2015. november)

C. 1317. Az \(\displaystyle ABCDE\) ötszög \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) csúcsánál levő belső szögek rendre \(\displaystyle 90^\circ\), \(\displaystyle 60^\circ\), \(\displaystyle 150^\circ\) és \(\displaystyle 150^\circ\), továbbá \(\displaystyle AB=2BC=\frac 43 AD\). Bizonyítsuk be, hogy az \(\displaystyle AE\) és \(\displaystyle CD\) egyenesek metszéspontját az \(\displaystyle AD\) és \(\displaystyle BC\) egyenesek metszéspontjával összekötő szakasz párhuzamos \(\displaystyle AB\)-vel.

(5 pont)

A beküldési határidő 2015. december 10-én LEJÁRT.

Megoldás. Készítsünk ábrát. Legyen az \(\displaystyle AB\) szakasz hossza \(\displaystyle 4x\), ekkor \(\displaystyle BC=2x\) és \(\displaystyle AD=3x\).

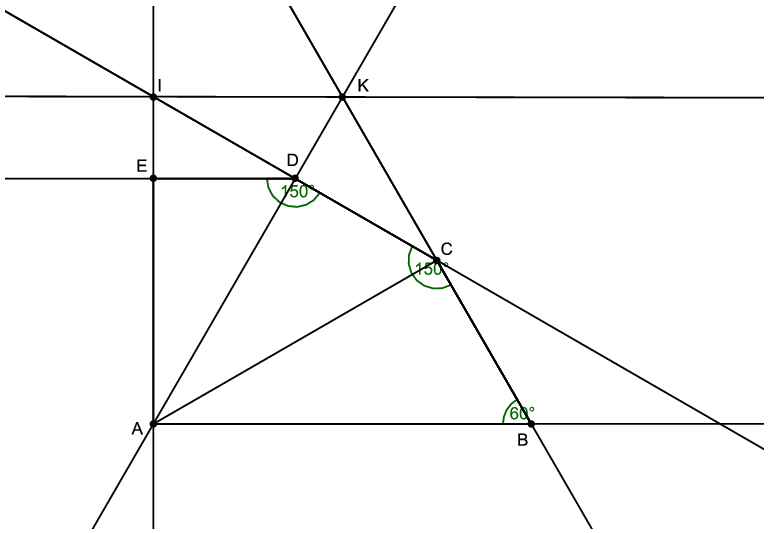
Ekkor az \(\displaystyle ABC\) háromszögben a \(\displaystyle B\) csúcsnál fekvő szög \(\displaystyle 60^{\circ}\)-os és \(\displaystyle AB=2BC\), így a háromszög egy szabályos háromszög fele, és \(\displaystyle BAC\angle=30^{\circ}\), \(\displaystyle BCA\angle=90^{\circ}\). Ebből egyrészt \(\displaystyle ICA\angle=150^{\circ}-90^{\circ}=60^{\circ}\), másrészt \(\displaystyle CAI\angle=90^{\circ}-30^{\circ}=60^{\circ}\) következik. Így az \(\displaystyle ACI\) háromszögben az \(\displaystyle A\) és a \(\displaystyle C\) csúcsnál lévő szög is \(\displaystyle 60^{\circ}\)-os, a háromszög szabályos. Oldalainak hossza \(\displaystyle AI=AC=\frac{\sqrt3}{2}\cdot AB=2\sqrt3 x\), ez egyben az \(\displaystyle I\) pont távolsága az \(\displaystyle AB\) egyenestől.

\(\displaystyle AD=3x=\frac{\sqrt3}{2}\cdot2\sqrt3 x\), ami éppen az \(\displaystyle ACI\) háromszög magasságának a hossza. Ezért \(\displaystyle AD\) az \(\displaystyle ACI\) szabályos háromszögben az \(\displaystyle A\) csúcsól kiinduló magasság, ami egyben szögfelező is. Ezért \(\displaystyle DAC\angle=30^{\circ}\). Ebből \(\displaystyle DAB\angle=DAC\angle+BAC\angle=30^{\circ}+30^{\circ}=60^{\circ}\), vagyis az \(\displaystyle ABK\) háromszögben az \(\displaystyle A\) és a \(\displaystyle B\) csúcsnál fekvő szög egyaránt \(\displaystyle 60^{\circ}\) és így a háromszög szabályos (ennek a háromszögnek a fele az \(\displaystyle ABC\) háromszög). Az \(\displaystyle ABK\) háromszögben a három magasság hossza egyenlő, vagyis \(\displaystyle K\) távolsága az \(\displaystyle AB\) egyenestől megegyezik \(\displaystyle AC\)-vel, amiről már tudjuk, hogy egyenlő \(\displaystyle AI\)-vel.

Tehát az \(\displaystyle I\) és a \(\displaystyle K\) pont távolsága az \(\displaystyle AB\) egyenestől ugyanakkora, vagyis \(\displaystyle IK||AB\).

Statisztika:

157 dolgozat érkezett.
5 pontot kapott:	94 versenyző.
4 pontot kapott:	14 versenyző.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	19 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	8 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2015. novemberi matematika feladatai