 |
A C. 1335. feladat (2016. január) |
C. 1335. Egy egységnyi oldalú, szabályos háromszög alapú gúla oldaléleinek hossza 2 egység. Mekkora a gúla kitérő éleinek távolsága?
(5 pont)
A beküldési határidő 2016. február 10-én LEJÁRT.
Megoldás. A gúla csúcsai legyenek \(\displaystyle A,B,C\) és \(\displaystyle D\). Legyen a \(\displaystyle {BC}\) oldal felezőpontja \(\displaystyle F\), az \(\displaystyle {ABC}\) háromszög súlypontja. Az \(\displaystyle {AD}\) és \(\displaystyle {BC}\) kitérő élek távolsága az \(\displaystyle F\) pontból az \(\displaystyle {AD}\) élre bocsátott merőleges szakasz hossza: \(\displaystyle {FM.}\)
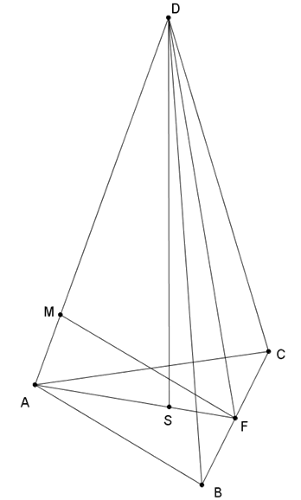
Az \(\displaystyle {AFD}\) háromszögben \(\displaystyle {AD}=2\), \(\displaystyle {AF}=\frac{\sqrt 3} 2\) (az egységnyi oldalú szabályos háromszög magassága). \(\displaystyle {FD}\) a gúla oldalháromszögének magassága:
\(\displaystyle {FD}=\sqrt{2^2-\left(\frac 1 2\right)^2}=\frac{\sqrt{15}} 2,\)
\(\displaystyle {AS}=\frac 2 3{AF}=\frac 2 3\cdot \frac{\sqrt 3} 2=\frac{\sqrt 3} 3.\)
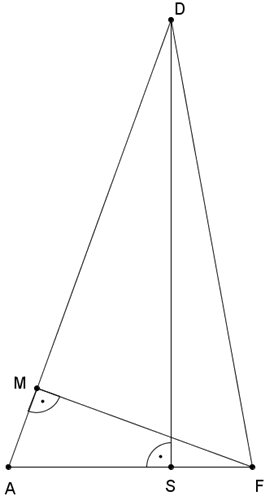
Az \(\displaystyle {ASD}\) derékszögű háromszögben
\(\displaystyle {SD}=\sqrt{2^2-\left(\frac{\sqrt 3} 3\right)^2}=\sqrt{\frac{11} 3}.\)
Az \(\displaystyle {ASD}\) és \(\displaystyle {AMF}\) derékszögű háromszögek hasonlóak, mert egy hegyesszögük közös, így
\(\displaystyle \frac{{FM}}{{AF}}=\frac{{SD}}{{AD}},\)
amiből \(\displaystyle {FM}=\frac{{SD}}{{AD}}{AF}=\frac{\sqrt{\frac{11} 3}} 2\frac{\sqrt 3} 2=\frac{\sqrt{11}} 4\,{\approx}\,0,8292\), ez a kitérő élek távolsága a gúlában.
Statisztika:
46 dolgozat érkezett. 5 pontot kapott: Balázs Ákos Miklós, Csorba Benjámin, Fülöp Ágota, Kasó Ferenc, Kiss Vivien Mercédesz, Kocsis Júlia, Kormányos Hanna Rebeka, Kósa Szilárd, Mészáros 01 Viktória, Nagy 911 Viktória, Novák Réka, Ondrik Ákos, Perger Kitti, Sallai Krisztina, Szajkó Gréta, Szauer Marcell, Tóth Adrián. 4 pontot kapott: Antal Márton, Csapó Márton, Csider Márk, Dankowsky Anna Zóra, Farkas Patrik, Földvári Benedek, Gera Dóra, Horváth András János, Józsa Dominik, Kovács Iván, Matusek Márton, Moldován Péter, Szücs Patrícia, Tar Viktor. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 4 versenyző.
A KöMaL 2016. januári matematika feladatai

