 |
A C. 1336. feladat (2016. február) |
C. 1336. Hányféleképpen lehet egy \(\displaystyle 6\times6\)-os négyzetet \(\displaystyle 1\times3\)-as téglalapokra feldarabolni?
(5 pont)
A beküldési határidő 2016. március 10-én LEJÁRT.
Megoldás. Induljunk el a darabolási lehetőségek leszámolásával attól az esettől, mikor minden \(\displaystyle 3\times1\) cm-es téglalap vízszintesen fekszik és fordítsunk egyre többet függőleges, álló helyzetbe.
1. eset: Minden téglalap fekvő helyzetben van: 1 lehetőség (1. ábra).
2. eset: 3 téglalap van álló helyzetben. Kevesebb nem lehet, mert különben nem tudjuk kitölteni a megmaradó helyet \(\displaystyle 3\times1\) cm-es téglalapokkal. A 3 db elfordított téglalap függőleges helyzete ugyanaz kell, hogy legyen. Ez a függőleges helyzet négyféle lehet. Mindegyik függőleges helyzet három sort határoz meg, az ebben a három sorban lévő három vízszintes téglalap egy \(\displaystyle 3\times3\)-as négyzetet alkot, aminek négyféle helyzete lehet. Ez tehát \(\displaystyle 4\cdot4=16\) lehetőség (1. ábra).
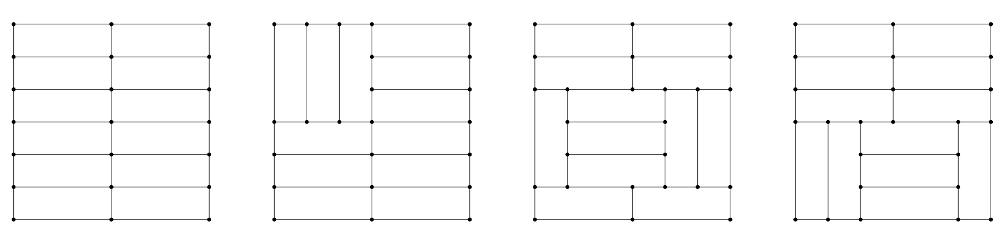
1. ábra
3. eset: 6 db téglalap van álló helyzetben. Ekkor 6 téglalap vízszintes helyzetben van. Összesen 4 db \(\displaystyle 3\times3\)-as négyzet képezhető belőlük. Ha az egyik elemeit, például egy vízszintes téglalapokból álló négyzet elemeit nem egymás mellett helyezzük el, akkor köztük egy \(\displaystyle 3\times3\)-as, függőleges téglalapokból álló négyzetnek kell lennie. Ennél a példánál kitöltünk egy 3 szélességű oszlopot, ami csak úgy lehetséges, ha a \(\displaystyle 6\times6\)-os négyzetet két, 3 szélességű oszlopra bontjuk szét, és a másik 3 szélességű oszlopban is található valahol egy \(\displaystyle 3\times3\)-as, függőleges téglalapokból álló négyzet. A fentiek alapján:
3.a eset: a 6 álló helyzetű téglalapból 2 db \(\displaystyle 3\times3\) cm-es négyzetet alkotunk, ezeket mozgathatjuk függőlegesen egymástól függetlenül 4-4 helyzetbe, ez \(\displaystyle 4\cdot4=16\) lehetőség (2. ábra).
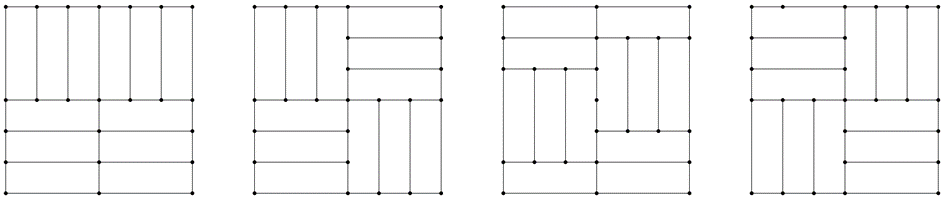
2. ábra
3.b. eset: 6 db téglalap van fekvő helyzetben egymás alatt balra. Ezekből 2 db \(\displaystyle 3\times3\) cm-es négyzet alkotunk, ezeket mozgathatjuk vízszintesen egymástól függetlenül 4-4 helyzetbe, ez \(\displaystyle 4\cdot4=16\) eset lenne, de azt a 2 esetet, mikor átlósan szélső helyzetben van a két négyzet, már a 3.a. esetbe beleszámoltuk. Ez tehát 14 további lehetőség (3. ábra).
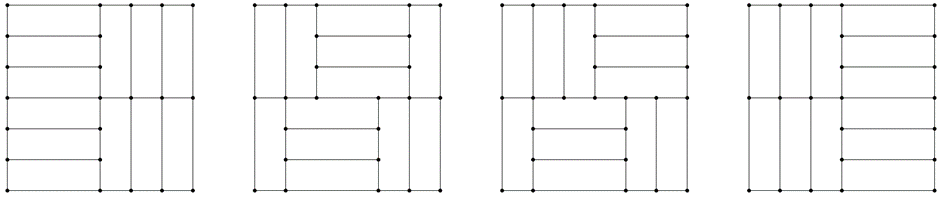
3. ábra
4. eset: 3 téglalap van fekvő és 9 álló helyzetben. Ez ugyanaz, mint a 2. eset, csak a fekvő és álló téglalapok szerepe felcserélődött. Tehát ez \(\displaystyle 4\cdot4=16\) lehetőség.
5. eset: Minden téglalap álló helyzetben van. Ez 1 lehetőség.
Összesen \(\displaystyle 1+16+16+14+16+1=64\) lehetőség van.
Statisztika:
70 dolgozat érkezett. 5 pontot kapott: Balázs Boglárka, Barta Gergely, Dávid Levente, Fajszi Bulcsú, Fekete Balázs Attila, Jedlovszky Pál, Kamenár Gyöngyvér, Mikulás Zsófia, Németh Csilla Márta, Paulovics Péter, Póta Balázs, Szécsi Adél Lilla, Szilágyi Éva, Tóth 111 Máté , Varga 157 Kristóf, Vlaszov Artúr, Weisz Máté. 4 pontot kapott: Braun Dániel, Édes Lili, Fraknói Ádám, Fucskár Patrícia, Jalsovszky Janka, Kovács 888 Anna, Maksa Gergő, Markó Anna Erzsébet, Marozsák Tóbiás , Márton Anna, Mayer Boglárka, Mohácsi Márton, Nagy 999 Benedek, Nagy Enikő, Nagy Viktor, Nanys Patrick, Négyessy Eszter, Pinke Andrea, Szalay Gergő, Tubak Dániel, Zsombó István. 3 pontot kapott: 13 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2016. februári matematika feladatai

