 |
A C. 1348. feladat (2016. március) |
C. 1348. Egy háromszögben az oldalak mérőszámai egymást követő egész számok, és a legnagyobb szög kétszer akkora, mint a legkisebb. Mekkorák a háromszög oldalai?
(5 pont)
A beküldési határidő 2016. április 11-én LEJÁRT.
I. megoldás. Legyenek a háromszög csúcsai \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\), a legkisebb szög \(\displaystyle \alpha\), a legnagyobb \(\displaystyle 2\alpha\). A háromszög oldalai legyenek \(\displaystyle a\), \(\displaystyle a-1\) és \(\displaystyle a+1\), ahol \(\displaystyle a \in \Bbb N^+\). Mivel egy háromszögben nagyobb oldallal szemben nagyobb szög van, ezért az \(\displaystyle a+1\) hosszúságú oldallal szemben van a \(\displaystyle 2\alpha\) nagyságú szög (1. ábra). Felezzük meg a \(\displaystyle 2\alpha\) nagyságú szöget. Messe a szögfelező az \(\displaystyle AB\) oldalt a \(\displaystyle D\) pontban.

1. ábra
Az \(\displaystyle AD\) szakaszt kifejezhetjük a szögfelező tétel felhasználásával arányos osztással:
\(\displaystyle AD=\frac{(a-1)(a+1)}{a-1+a}=\frac{(a-1)(a+1)}{2a-1}.\)
Az \(\displaystyle ACD\) és az \(\displaystyle ABC\) háromszögek hasonlóak, mert egy szögük közös, a másik kettő pedig \(\displaystyle \alpha\), \(\displaystyle 2\alpha\). Ezért \(\displaystyle \frac{AD}{a-1}=\frac{a-1}{a+1}\).
\(\displaystyle AD\) előző értékét behelyettesítve: \(\displaystyle \frac{a+1}{2a-1}=\frac{a-1}{a+1}\).
Átszorozva és rendezve:
\(\displaystyle (a+1)^2=(2a-1)(a-1),\)
\(\displaystyle a^2+2a+1=2a^2-3a+1,\)
\(\displaystyle 0=a^2-5=a(a-5).\)
A két megoldás közül \(\displaystyle a=5\) felel meg a feladat feltételeinek. Tehát a háromszög oldalainak hossza 4, 5 és 6.
II. megoldás. A 2. ábra jelölései alapján írjuk fel a szinusz tételt:
\(\displaystyle \frac{a+1}{a-1}=\frac{\sin2\alpha}{\sin\alpha}=\frac{2\sin\alpha\cos\alpha}{\sin\alpha}=2\cos\alpha.\)
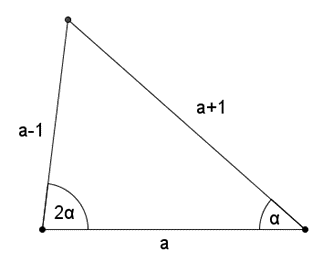
2. ábra
A koszinusz tétel alapján: \(\displaystyle \cos\alpha=\frac{a^2+(a+1)^2-(a-1)^2}{2a(a+1)} =\frac{a^2+4a}{2a(a+1)}=\frac{a+4}{2(a+1)}\).
Ezekből \(\displaystyle \frac{a+1}{a-1}=\frac{2(a+4)}{2(a+1)}=\frac{a+4}{a+1}\), ahonnan \(\displaystyle (a+1)^2=(a-1)(a+4)\), vagyis \(\displaystyle a^2+2a+1=a^2+3a-4\), azaz \(\displaystyle a=5\).
Tehát a háromszög oldalai 4, 5 és 6.
Statisztika:
31 dolgozat érkezett. 5 pontot kapott: Csapó Márton, Csorba Benjámin, Erdélyi Janka, Földvári Benedek, Gera Dóra, Horváth 999 Viktória, Horváth András János, Kasó Ferenc, Kocsis Júlia, Kormányos Hanna Rebeka, Matusek Márton, Moldován Péter, Nagy 911 Viktória, Perger Kitti, Sudár Ákos, Szabó Alexandra, Szauer Marcell, Szécsényi Júlia, Tatai Mihály, Török Réka . 4 pontot kapott: Dankowsky Anna Zóra, Hack Aliz, Józsa Dominik, Komoróczy Ádám, Ványi Virág. 3 pontot kapott: 4 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2016. márciusi matematika feladatai

