 |
A C. 1356. feladat (2016. április) |
C. 1356. Az \(\displaystyle ABCDEFGH\) kockában legyen \(\displaystyle K\) az \(\displaystyle AB\), \(\displaystyle L\) a \(\displaystyle CG\), \(\displaystyle M\) pedig az \(\displaystyle EH\) él felezőpontja. Hányad része az \(\displaystyle FKLM\) tetraéder térfogata a kocka térfogatának?
(5 pont)
A beküldési határidő 2016. május 10-én LEJÁRT.
Megoldás.
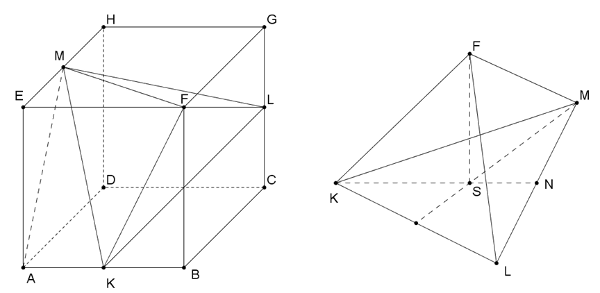
A bal oldali ábra jelöléseit használva, legyen \(\displaystyle AB= 2\) egység, ekkor \(\displaystyle AK=EM=1\).
Az \(\displaystyle AEM\) derékszögű háromszögre felírva a Pitagorasz-tételt: \(\displaystyle AM^2=EM^2+AE^2\), amiből \(\displaystyle AM=\sqrt{1^2+2^2}=\sqrt5\).
Mivel \(\displaystyle AK\) merőleges az \(\displaystyle ADHE\) síkra, így annak összes egyenesére is merőleges. Tehát az \(\displaystyle MAK\) háromszög \(\displaystyle A\) csúcsánál derékszög van, a háromszögre felírható a Pitagorasz-tétel: \(\displaystyle MK^2=AK^2+AM^2\), amiből \(\displaystyle MK=\sqrt{1+5}=\sqrt6\).
Ugyanígy \(\displaystyle KL=LM=\sqrt6\), tehát a \(\displaystyle KLM\) háromszög szabályos.
Mivel \(\displaystyle FK=FL=FM=\sqrt5\), ezért \(\displaystyle FKLM\) szabályos háromoldalú gúla.
A kocka térfogata: \(\displaystyle V_k=8\).
A jobb oldali ábra jelöléseit használva: \(\displaystyle KS=\frac23 KN=\frac23 KL\cdot\frac{\sqrt3}{2}=\frac{\sqrt3}{3}\cdot\sqrt6=\sqrt2\),\(\displaystyle \,\) \(\displaystyle FS^2=KF^2-KS^2\), amiből \(\displaystyle FS=\sqrt{5-2}=\sqrt3\).
Ezeket felhasználva gúla térfogata:
\(\displaystyle V_g=\frac{T_{KLM}\cdot FS}{3}=\frac{KL^2\cdot\sqrt3}{4}\cdot \frac{FS}{3}=\frac{6\cdot\sqrt3\cdot\sqrt3}{12}=\frac32.\)
A gúla és a kocka térfogatának aránya:
\(\displaystyle \frac{V_g}{V_k} =\frac{\frac32}{8}=\frac{3}{16}.\)
Statisztika:
28 dolgozat érkezett. 5 pontot kapott: Antal Márton, Csapó Márton, Csorba Benjámin, Horváth András János, Kocsis Júlia, Kormányos Hanna Rebeka, Kósa Szilárd, Matusek Márton, Nagy 911 Viktória, Ondrik Ákos, Simon Ákos, Sudár Ákos, Szabó Alexandra, Tatai Mihály. 4 pontot kapott: Bőzsöny András, Fülöp Ágota, Kasó Ferenc, Kiss Vivien Mercédesz, Kovács Iván, Lévay Mátyás, Perger Kitti, Szajkó Gréta, Török Réka . 3 pontot kapott: 4 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2016. áprilisi matematika feladatai

