 Problem C. 1367. (September 2016)
Problem C. 1367. (September 2016)
C. 1367. The convex octagon \(\displaystyle ABCDEFGH\) has a centre of symmetry. Prove that the sum of the areas of the quadrilaterals \(\displaystyle ABEF\), \(\displaystyle BCFG\), \(\displaystyle CDGH\) and \(\displaystyle DEHA\) is twice the area of the octagon.
(5 pont)
Deadline expired on October 10, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel a nyolcszög középpontosan szimmetrikus, az \(\displaystyle ABEF\) négyszög paralelogramma, így a \(\displaystyle BF\) átló felezi a területét. Az \(\displaystyle ABF\) háromszög területét pedig az \(\displaystyle AO\) súlyvonala felezi.
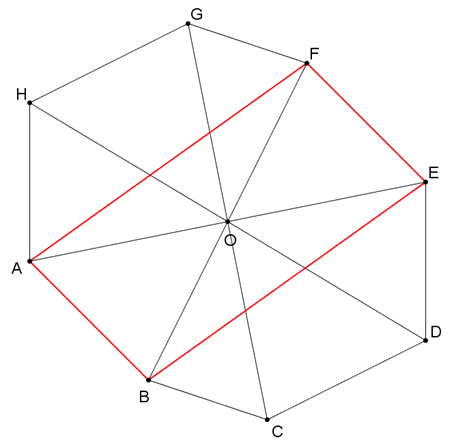
Ezért \(\displaystyle T_{ABO}=\frac{T_{ABEF}}{4}\). A szimmetria miatt \(\displaystyle T_{ABO}=T_{EFO}\), így \(\displaystyle T_{ABO}+T_{EFO}=\frac{T_{ABEF}}{2}\), vagyis \(\displaystyle T_{ABEF}=2(T_{ABO}+T_{EFO})\).
Hasonló állításokat láthatunk be a \(\displaystyle BCFG\), \(\displaystyle CDGH\) és \(\displaystyle DEHA \) paralelogrammákra.
A nyolcszög területe az \(\displaystyle ABO\), \(\displaystyle BCO\),…, \(\displaystyle HAO\) részháromszögek területének összege. A négy paralelogramma területének összege pedig ezen háromszögek területösszegének kétszerese.
Tehát \(\displaystyle T_{ABEF}+T_{BCFG}+T_{CDGH}+T_{DEHA}=2\cdot T_{ABCDEFGH}\).
Megjegyzés. Nagyon sokan rosszul értelmezték a feladatot és szabályos (esetleg tengelyesen szimmetrikus) nyolcszögre oldották meg a feladatot. Ők 0 pontot kaptak.
Statistics:
229 students sent a solution. 5 points: 115 students. 4 points: 27 students. 3 points: 5 students. 2 points: 6 students. 1 point: 5 students. 0 point: 69 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, September 2016
