 Problem C. 1369. (September 2016)
Problem C. 1369. (September 2016)
C. 1369. The coordinates of the centroid of a triangle are \(\displaystyle \left(5;-\frac{5}{3}\right)\), its orthocentre is \(\displaystyle (3;-1)\), and one vertex is \(\displaystyle (7;3)\). Find the coordinates of the other two vertices.
(5 pont)
Deadline expired on October 10, 2016.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen \(\displaystyle F\) az \(\displaystyle a\) oldal felezőpontja és használjuk az ábra jelöléseit.
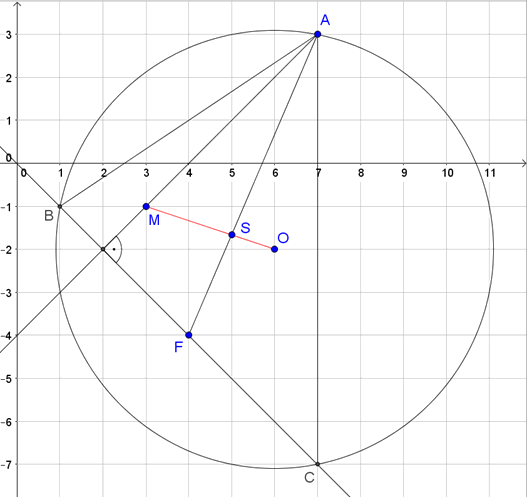
Ekkor az \(\displaystyle S\) súlypont 2:1 arányban osztja az \(\displaystyle AF\) szakaszt. Ebből \(\displaystyle F\) koordinátái kiszámíthatók: \(\displaystyle \frac{2x_F+7}{3}=5\), \(\displaystyle \frac{2y_F+3}{3}=-\frac53\), amiből \(\displaystyle x_F=4\) és \(\displaystyle y_F=-4\), vagyis \(\displaystyle F(4;-4)\).
Az \(\displaystyle a\) oldal egyenese átmegy az \(\displaystyle F\) ponton és merőleges az \(\displaystyle AM\) egyenesre, ezért egyik pontja \(\displaystyle F(4;-4)\), normálvektora \(\displaystyle \overrightarrow{MA}=(4;4)\), így egyenlete \(\displaystyle x+y=0\), vagyis \(\displaystyle y=-x\).
Az \(\displaystyle M\) magasságpont, az \(\displaystyle S\) súlypont és \(\displaystyle O\), a körülírt kör középpontja a háromszög Euler-egyenesén vannak és az \(\displaystyle S\) pont 2:1 arányban osztja az \(\displaystyle MO\) szakaszt. Ebből az \(\displaystyle O\) pont koordinátái kiszámíthatók: \(\displaystyle \frac{2x_O+3}{3}=5\), \(\displaystyle \frac{2y_O-1}{3}=-\frac53\), amiből \(\displaystyle x_O=6\) és \(\displaystyle y_O=-2\), vagyis \(\displaystyle O(6;-2)\).
A háromszög köré írt kör sugara: \(\displaystyle r=|\overrightarrow{OA}|=\sqrt{(7-6)^2+(3+2)^2}=\sqrt{26}\), egyenlete: \(\displaystyle (x-6)^2+(y+2)^2=26\).
A \(\displaystyle B\) és \(\displaystyle C\) csúcsok koordinátáit az \(\displaystyle a\) oldalegyenes és a kör metszéspontjai adják:
\(\displaystyle (x-6)^2+(y+2)^2=26,\)
\(\displaystyle y=-x.\)
Behelyettesítve:
\(\displaystyle (x-6)^2+(2-x)^2=26,\)
\(\displaystyle x^2-12x+36+4-4x+x^2=26.\)
Rendezve:
\(\displaystyle 2x^2-16x+14=0,\)
\(\displaystyle x^2-8x+7=0.\)
Megoldások: \(\displaystyle x_1=1\), \(\displaystyle x_2=7\). A megfelelő \(\displaystyle y\) koordináták: \(\displaystyle y_1=-1\), \(\displaystyle y_2=-7\).
Tehát a háromszög másik két csúcsának koordinátái: \(\displaystyle B(1;-1)\) és \(\displaystyle C(7;-7\)).
Statistics:
90 students sent a solution. 5 points: 51 students. 4 points: 4 students. 3 points: 9 students. 2 points: 6 students. 1 point: 15 students. 0 point: 4 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, September 2016
