 Problem C. 1371. (October 2016)
Problem C. 1371. (October 2016)
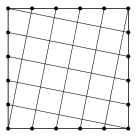
C. 1371. Each side of a unit square is divided into \(\displaystyle n\) equal parts, and the division points of opposite sides are connected in a shifted manner, as shown in the diagram (representing the case of \(\displaystyle n=5\)). Prove that it is possible to reassemble these pieces to get \(\displaystyle n^2+1\) smaller congruent squares.
(5 pont)
Deadline expired on November 10, 2016.
Sorry, the solution is available only in Hungarian. Google translation
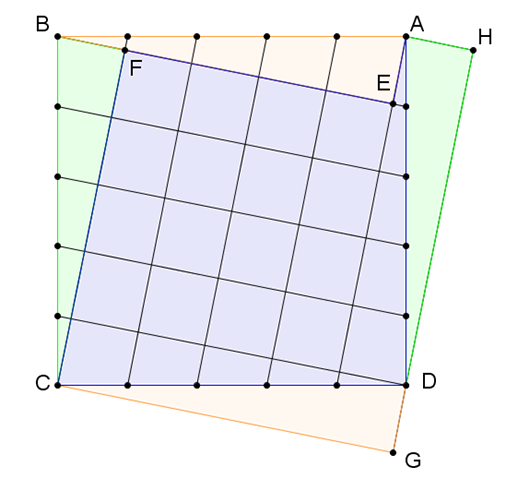
Megoldás. Az 1. ábra jelöléseit használva, toljuk el az \(\displaystyle ABE\) háromszöget \(\displaystyle \overrightarrow{BC}\) vektorral, így kapjuk a \(\displaystyle CDG\) háromszöget; majd a \(\displaystyle BCF\) háromszöget \(\displaystyle \overrightarrow{BA}\) vektorral, így az \(\displaystyle ADH\) háromszöghöz jutunk. Ezzel átdaraboltuk az eredeti \(\displaystyle ABCD\) négyzet területét az \(\displaystyle AEFCGH\) sokszögbe.
1. ábra
A 2. ábra jelöléseit használva, legyen az \(\displaystyle FE\) és a \(\displaystyle GH\) egyenes metszéspontja \(\displaystyle K\). Ekkor az \(\displaystyle FCGK\) négyszög négyzet, ami \(\displaystyle n^2\) kisebb négyzetből áll és ezekkel egybevágó az \(\displaystyle AEKH\) kis négyzet.
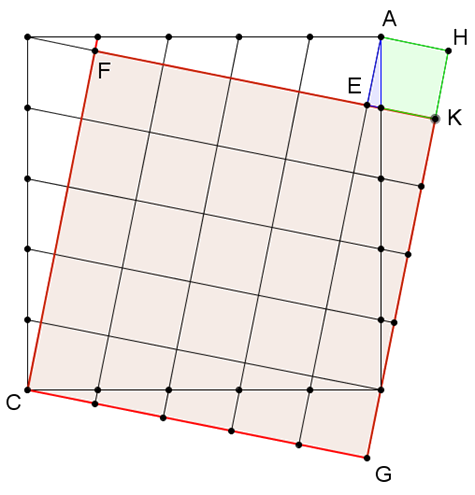
Ezzel beláttuk, hogy az eredeti \(\displaystyle ABCD\) négyzet átdarabolásával \(\displaystyle n^2+1\) kisebb négyzetet lehet összerakni.
Statistics:
195 students sent a solution. 5 points: 146 students. 4 points: 36 students. 3 points: 8 students. 2 points: 3 students. 1 point: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, October 2016
