Problem C. 1372. (October 2016)

C. 1372. A regular octagon is formed by cutting off the corners of a square in the appropriate way. Which is greater: the percentage decrease of the perimeter of the square or the percentage decrease of its area?

(5 pont)

Deadline expired on November 10, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A négyzet oldala legyen \(\displaystyle a=1\), a nyolcszög oldala legyen \(\displaystyle b\).

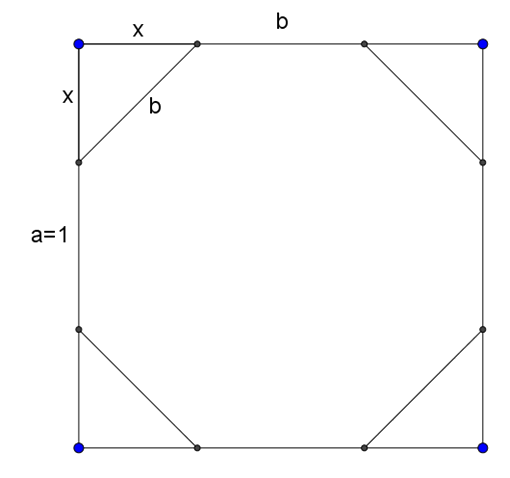
Az ábra alapján \(\displaystyle b\)-re a következő egyenletet tudjuk felírni:

\(\displaystyle 1-2x=x\sqrt2.\)

Rendezve és gyöktelenítve a nevezőt:

\(\displaystyle x=\frac{1}{2+\sqrt2}=\frac{2-\sqrt2}{2}.\)

A négyzet kerülete \(\displaystyle K_4=4\), területe \(\displaystyle T_4=1\).

A nyolcszög kerülete: \(\displaystyle K_8=8b=8x\sqrt2=4\sqrt2(2-\sqrt2)\).

A nyolcszög területe:

\(\displaystyle T_8=1-2x^2=1-2\left(\frac{2-\sqrt2}{2}\right)^2= 1-\frac{4-4\sqrt2+2}{2}=1-(2-2\sqrt2+1)=2\sqrt2-2.\)

Vizsgáljuk meg a két arányt.

\(\displaystyle \frac{K_8}{K_4} =\frac{4\sqrt2(2-\sqrt2)}{4}=2\sqrt2-2.\)

\(\displaystyle \frac{T_8}{T_4} =\frac{2\sqrt2-2}{1}=2\sqrt2-2.\)

Tehát a négyzet kerülete és területe egyenlő arányban csökken.

Statistics:

221 students sent a solution.
5 points:	151 students.
4 points:	21 students.
3 points:	23 students.
2 points:	12 students.
1 point:	6 students.
0 point:	8 students.

Problems in Mathematics of KöMaL, October 2016