Problem C. 1377. (October 2016)

C. 1377. An isosceles triangle of perimeter 20 cm is rotated about its base. What is the maximum possible volume of the double cone obtained?

(5 pont)

Deadline expired on November 10, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen az \(\displaystyle ABC\) egyenlő szárú háromszög alapja \(\displaystyle a\), szára pedig \(\displaystyle b\), az ábra szerint.

Tudjuk, hogy a kerülete 20 cm, így \(\displaystyle K=a+2b=20\), amiből \(\displaystyle b=10-a/2\).

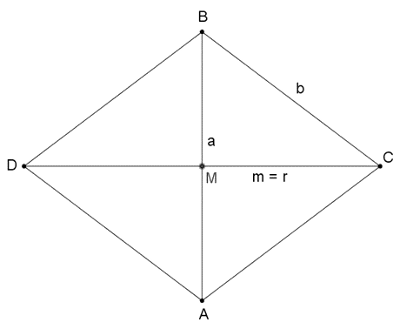
Az egyik forgáskúp alkotója \(\displaystyle b\), magassága \(\displaystyle a/2\), alapkörének sugara \(\displaystyle r=m\), a háromszög alaphoz tartozó magassága.

Az \(\displaystyle BCM\) derékszögű háromszögben a Pitagorasz-tétel alapján:

\(\displaystyle r=\sqrt{b^2-\left(\frac a2\right)^2}=\sqrt{\left(10-\frac a2\right)^2-\left(\frac a2\right)^2 }=\sqrt{100-10a}.\)

A kettőskúp térfogata:

\(\displaystyle V=\frac{\pi\cdot r^2\cdot a}{3}=\frac{\pi\cdot(100-10a)\cdot a}{3}=-\frac{10\pi}{3} a^2+\frac{100\pi}{3} a=\frac{10\pi}{3}(-a^2+10a).\)

Elegendő az \(\displaystyle f(a)=-a^2+10a\) függvény maximumát vizsgálni.

\(\displaystyle f(a)=-a^2+10a=-(a^2-10a+25)+25=-(a-5)^2+25.\)

A maximum \(\displaystyle a=5\) esetén van, értéke 25. Ezért a kettős forgáskúp térfogata legfeljebb \(\displaystyle V_{max}=\frac{250\pi}{3}\) lehet.

Statistics:

92 students sent a solution.
5 points:	Agócs Katinka, Benkő Glória, Boros Bence, Demeter Gergő, Erdődi Ádám Károly, Galvács Ákos, Gera Dóra, Karácsony Márton, Kocsis Ábel, Kocsis Júlia, Kormányos Hanna Rebeka, Mácz Andrea, Magyar 257 Boglárka, Malák Péter, Márki Péter, Mészáros Melinda, Nagy Enikő, Nagy Olivér, Németh Csilla Márta, Ondrik Ákos, Pál Regő, Perényi Gellért, Radó Albert, Simon Ákos, Surján Anett, Szabadfalvi Dániel, Szabó Alexandra, Szalay Dorottya, Szilágyi Botond, Tanács Viktória, Tatai Mihály, Tolmácsi Ágnes, Török Attila, Veres Károly, Zeller Doroti, Zsombó István.
4 points:	30 students.
3 points:	14 students.
2 points:	3 students.
1 point:	4 students.
0 point:	3 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, October 2016