Problem C. 1379. (November 2016)

C. 1379. A certain cyclic trapezium has an inscribed circle. Prove that one of the two line segments joining the points of tangency on the opposite sides is the geometric mean of the bases, and the other is the harmonic mean.

(5 pont)

Deadline expired on December 12, 2016.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az ábra jelöléseit felhasználva a trapéz \(\displaystyle AD\) szárán lévő szögekre \(\displaystyle α+δ=180°\). Így \(\displaystyle \alpha/2+\delta/2=90^{\circ}\). Ezért az \(\displaystyle AOD\) háromszög derékszögű, az átfogóhoz tartozó magassága \(\displaystyle r\). Az érintési szakaszok egyenlősége miatt \(\displaystyle AH=AE=\frac a2\), \(\displaystyle DH=DG=\frac c2\) és így \(\displaystyle AD=\frac{a+c}{2}\). Alkalmazzuk a magasságtételt a háromszögben: \(\displaystyle r=\sqrt{\frac a2\cdot\frac c2}=\frac{\sqrt{ac}}{2}\).

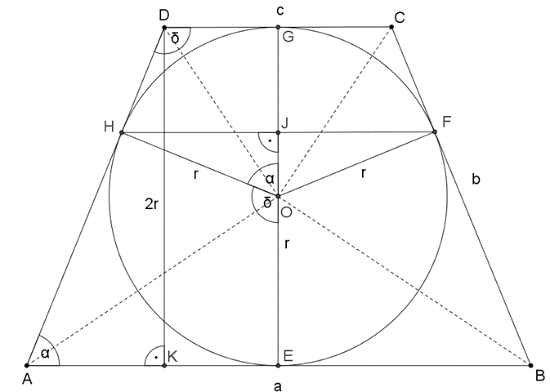
Tehát az \(\displaystyle E\) és \(\displaystyle G\) érintési pontok távolsága: \(\displaystyle EG=2r=\sqrt{ac}\), ami a két párhuzamos oldal mértani közepe.

A \(\displaystyle DHOG\) négyszögben \(\displaystyle DGO∡=DHO∡=90^{\circ}\), tehát a négyszög húrnégyszög, és így \(\displaystyle HOG∡=180^{\circ}-δ=α\).

Az \(\displaystyle AKD\) derékszögű háromszögben \(\displaystyle \sin α=\frac{DK}{AD}=\frac{2r}{\frac{a+c}{2}}\).

Ezt felhasználva a \(\displaystyle HOJ\) derékszögű háromszögben \(\displaystyle \frac{HF}{2}=HJ=r\cdot \sin α=r\cdot \frac{2r}{\frac{a+c}{2}}=\frac{4r^2}{a+c}=\frac{ac}{a+c}\).

Tehát a másik két érintési pont távolsága: \(\displaystyle HF=\frac{2ac}{a+c}=\frac{2}{\frac1a+\frac1c}\), ami éppen a két párhuzamos oldal harmonikus közepe.

Statistics:

124 students sent a solution.
5 points:	95 students.
4 points:	3 students.
3 points:	12 students.
2 points:	1 student.
0 point:	10 students.
Unfair, not evaluated:	3 solutionss.

Problems in Mathematics of KöMaL, November 2016