Problem C. 1386. (December 2016)

C. 1386. How many different convex figures can be put together out of four congruent isosceles right-angled triangles?

(5 pont)

Deadline expired on January 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Két háromszöget vagy az átfogójuknál, vagy a befogójuknál fogva lehet összeilleszteni. Ez utóbbira kétféle lehetőség is van.

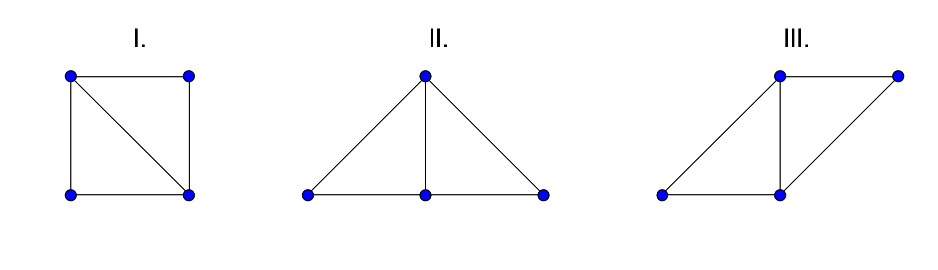
Az így kapott négyszögekből úgy illeszthető össze konvex síkidom, ha azonos hosszúságú oldalak mentén illesztjük őket össze.

Két darab I-es típust egyféle módon rakhatunk össze. Az I-esnek és a II-esnek nincs azonos hosszú oldala. Az I-es és a III-ast is (tükrözés erejéig) egyféle módon illeszthetjük össze, azonban a kapott síkidom konkáv.

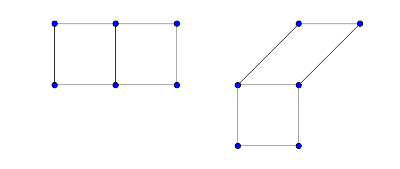
Két darab II-es típusút háromféleképp rakhatunk össze: az átfogójuknál érintkezve, vagy a befogónál, utóbbira két lehetőség is van. Egy II-es és egy III-as típusút a II-es típusú befogójánál érintkezve, a kapott két idomból egy lesz konvex.

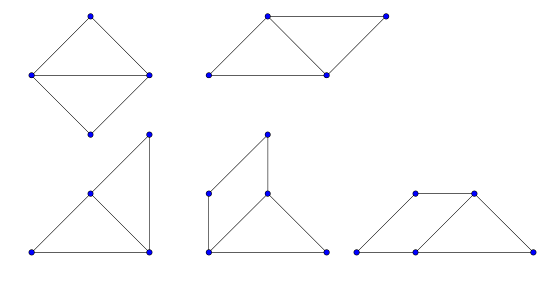
Végül, két III-as típusút vagy a rövidebb, vagy a hosszabb oldalnál illeszthetünk össze, mindkettőre két lehetőség van. Itt két konvex idomot kapunk, azonban az egyik már szerepelt két II-es típusú összeillesztésekor.

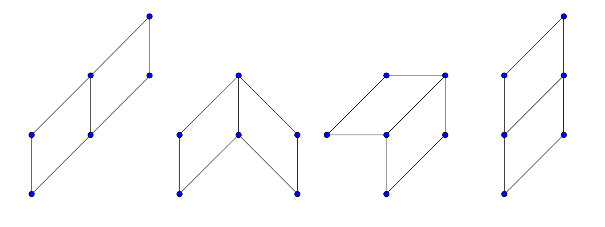
Tehát hat különböző konvex síkidomot lehet összeállítani a négy darab egybevágó egyenlő szárú derékszögű háromszögből. Egy derékszögű háromszöget, egy négyzetet, egy téglalapot, kétféle paralelogrammát és egy trapézt.

Statistics:

164 students sent a solution.
5 points:	Andó Viola, Balog 518 Lóránd, Barta Ákos, Böcskei Balázs, Dékány Barnabás, Dobák Dániel, Dudás Dominik, Földvári Ádám Dávid, Fülöp Dorottya Száva, Füredi Erik Benjámin, Gárdonyi Csilla Dóra, Gilicze Márton, Hajnal Lilla Viola, Harmath Eszter, Hervay Bence, Jánosdeák Márk, Keltai Dóra, Kertész Ferenc, Kinyó Kincső, Klučka Vivien, Kocsmár Martin, Kolláth István Tibor, Kovács 111 Máté, Kovács-Deák Zsombor, Mikulás Zsófia, Misik Márton, Nagy 999 Benedek, Nagy Csaba Jenő, Nagy Gábor János, Németh 728 Ágnes Sára, Pálvölgyi Szilveszter, Pinke Andrea, Rubovszky Cecília , Sal Dávid, Tirpák Péter, Vanya Dóra, Varga Levente, Veres Zsófi, Virág Levente, Weisz Máté, Weisz Viktória, Williams Hajna.
4 points:	33 students.
3 points:	40 students.
2 points:	35 students.
1 point:	8 students.
0 point:	5 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, December 2016