 Problem C. 1388. (December 2016)
Problem C. 1388. (December 2016)
C. 1388. The front and back edges of a rectangular billiards table are 90 cm long, while the left and right edges are 180 cm long. A ball situated 10 cm from the front edge and 15 cm from the left edge is hit. Rebounding from the front edge, then from the right edge, it rolls along the shortest possible path into the hole of the back left corner. What is the total distance covered by the ball until it sinks in the hole? (Ignore the size of the ball and of the hole.)
(Proposed by F. Olosz, Szatmárnémeti)
(5 pont)
Deadline expired on January 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen a biliárdasztal a \(\displaystyle DEFG\) téglalap. A golyó az \(\displaystyle A\) pontból indul, ütközik az \(\displaystyle EF\) oldallal a \(\displaystyle B\) pontban, majd az \(\displaystyle FG\) oldallal a \(\displaystyle C\) pontban, és a \(\displaystyle D\) pontban betalál a lyukba. Tükrözzük a \(\displaystyle DEFG\) téglalapot az \(\displaystyle EF\) oldalára, majd a keletkező \(\displaystyle EHIF\) téglalapot az \(\displaystyle IF\) oldalára. A második tükrözés eredménye az \(\displaystyle FIJK\) téglalap. A \(\displaystyle D\) lyuk kétszeres tükrözés utáni képe a \(\displaystyle J\) pont.
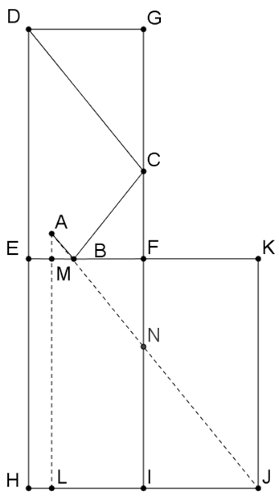
A golyó legrövidebb útja az \(\displaystyle A\)-tól \(\displaystyle J\)-ig az \(\displaystyle AJ\) egyenes szakasz. Így a \(\displaystyle B\) pont az \(\displaystyle EF\) és az \(\displaystyle AJ\) szakasz metszéspontja, a \(\displaystyle C\) pont pedig az \(\displaystyle FI\) és \(\displaystyle AJ\) szakaszok \(\displaystyle N\) metszéspontjának tükörképe az \(\displaystyle EF\) egyenesre.
A golyó útja az \(\displaystyle AJ\) szakasz hosszával egyezik meg, ami az \(\displaystyle ALJ\) derékszögű háromszög átfogója.
A feladat szövege szerint \(\displaystyle EF=90\) cm, \(\displaystyle DE=EH=ML=180\) cm, \(\displaystyle AM=10\) cm, \(\displaystyle EM=15\) cm, így \(\displaystyle AL=AM+ML=190\) cm, \(\displaystyle LJ=2EF-EM=165\) cm. Ebből
\(\displaystyle AJ=\sqrt{AL^2+LJ^2}\approx 251,64\mathrm{~cm}.\)
Tehát a golyó \(\displaystyle 251,64\) cm hosszú utat fut be a lyukig.
Statistics:
211 students sent a solution. 5 points: 164 students. 4 points: 4 students. 3 points: 22 students. 2 points: 8 students. 1 point: 7 students. 0 point: 6 students.
Problems in Mathematics of KöMaL, December 2016
