Problem C. 1389. (December 2016)

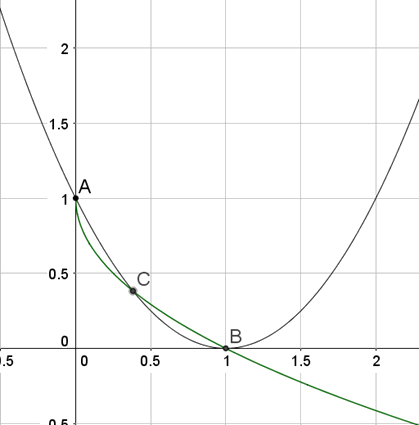
C. 1389. Find the common points of the curves of equations \(\displaystyle y={(x-1)}^2\) and \(\displaystyle y=1-\sqrt x\,\).

(5 pont)

Deadline expired on January 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Azokat a pontokat keressük, melyek \(\displaystyle x\) koordinátájára teljesül az alábbi egyenlet:

\(\displaystyle (x-1)^2=1-\sqrt x.\)

Mivel negatív számoknak nincs valós négyzetgyöke, így \(\displaystyle 0≤x\), másrészt az egyenlet bal oldala nem negatív, így a jobb oldalnak is annak kell lenni, így \(\displaystyle \sqrt x≤1\), vagyis \(\displaystyle x≤1\). Tehát tudjuk, hogy \(\displaystyle 0≤x≤1\).

A négyzetre emelést elvégezve, az egyenlet mindkét oldalából 1-et levonva és rendezve:

\(\displaystyle -x^2+2x=\sqrt x.\)

Mivel az \(\displaystyle x\)-re vonatkozó kikötés miatt mindkét oldal nemnegatív, ekvivalens átalakítás, ha mindkét oldalt négyzetre emeljük:

\(\displaystyle x^4-4x^3+4x^2=x.\)

Bal oldalra rendezve és \(\displaystyle x\)-t kiemelve:

\(\displaystyle x\cdot(x^3-4x^2+4x-1)=0.\)

Láthatjuk, hogy \(\displaystyle x=0\) mellett \(\displaystyle x=1\) is megoldás, ezért \(\displaystyle (x-1)\) a harmadfokú tagból kiemelhető:

\(\displaystyle x\cdot(x-1)(x^2-3x+1)=0.\)

A másodfokú kifejezés akkor lesz nulla, ha \(\displaystyle x_3=\frac{3-\sqrt5}{2}\) vagy \(\displaystyle x_4=\frac{3+\sqrt5}{2}\). Utóbbi azonban 1-nél nagyobb szám, így nem felel meg a kikötésnek.

Így a megoldások: \(\displaystyle x_1=0\), \(\displaystyle x_2=1\), \(\displaystyle x_3=\frac{3-\sqrt5}{2}\). Tehát három közös pontja van a görbéknek: \(\displaystyle A(0;1)\), \(\displaystyle B(1;0)\) és \(\displaystyle C\left(\frac{3-\sqrt5}{2};\frac{3-\sqrt5}{2}\right)\), ugyanis

\(\displaystyle \left(\frac{3-\sqrt5}{2}-1\right)^2=\frac{9-6\sqrt5+5}{4}-3+\sqrt5+1=\frac{14-6\sqrt5}{4}+\frac{-8+4\sqrt5}{4}=\frac{6-2\sqrt5}{4}=\frac{3-\sqrt5}{2}.\)

Statistics:

226 students sent a solution.
5 points:	101 students.
4 points:	53 students.
3 points:	14 students.
2 points:	12 students.
1 point:	36 students.
0 point:	8 students.
Unfair, not evaluated:	2 solutionss.

Problems in Mathematics of KöMaL, December 2016