 Problem C. 1395. (January 2017)
Problem C. 1395. (January 2017)
C. 1395. The length of one side of a parallelogram \(\displaystyle ABCD\) is twice the length of the other side. Determine the ratio of the area of the parallelogram formed by the interior angle bisectors to the area of \(\displaystyle ABCD\).
(5 pont)
Deadline expired on February 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Felezzük meg a paralelogramma hosszabb oldalait. Az ábra jelöléseit használva, legyen az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle E\), a \(\displaystyle DC\) oldalé pedig \(\displaystyle F\). \(\displaystyle EF\) a paralelogramma középvonala, így \(\displaystyle AD=EF=BC\) és \(\displaystyle AD||EF||BC\).
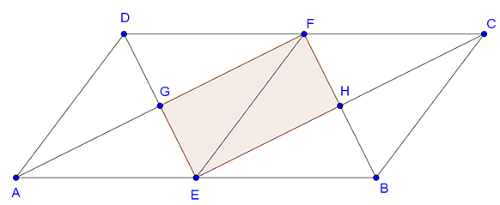
Ezért az \(\displaystyle EF\) szakasz a paralelogrammát két rombuszra osztja, hiszen \(\displaystyle AE=AD\) és \(\displaystyle EB=BC\) és a szemközti oldalak párhuzamosak. A paralelogramma belső szögfelezői egyben az \(\displaystyle AEFD\) és \(\displaystyle BCFE\) rombuszok átlói, mivel a rombusz átlói szögfelezők. Az átlók, vagyis a szögfelezők mindkét rombuszon belül merőlegesek egymásra és a rombuszokat 4-4 db egybevágó derékszögű háromszögre bontják. Így a paralelogramma 8 db ilyen háromszögből áll. A szögfelezők által meghatározott \(\displaystyle EHFG\) paralelogramma téglalap, és 2 db ilyen derékszögű háromszögből áll.
Tehát az \(\displaystyle EHFG\) és az \(\displaystyle ABCG\) paralelogrammák területének aránya: \(\displaystyle \frac 28=\frac 14\).
Statistics:
209 students sent a solution. 5 points: 184 students. 4 points: 12 students. 3 points: 1 student. 1 point: 8 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, January 2017
