Problem C. 1404. (February 2017)

C. 1404. \(\displaystyle D\) is the foot of the perpendicular drawn to side \(\displaystyle BC\) of an isosceles triangle \(\displaystyle ABC\) from the midpoint \(\displaystyle F\) of base \(\displaystyle AB\). The midpoint of line segment \(\displaystyle FD\) is \(\displaystyle G\). Prove that \(\displaystyle AD\) is perpendicular to \(\displaystyle CG\).

(5 pont)

Deadline expired on March 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit. Legyen a \(\displaystyle BD\) szakasz felezőpontja \(\displaystyle H\), így \(\displaystyle FH\) a \(\displaystyle BFD\) háromszög súlyvonala. A \(\displaystyle DCF\) és \(\displaystyle BFD\) derékszögű háromszögek hasonlóak, mert megfelelő hegyesszögeik merőleges szárú szögpárokat képeznek.

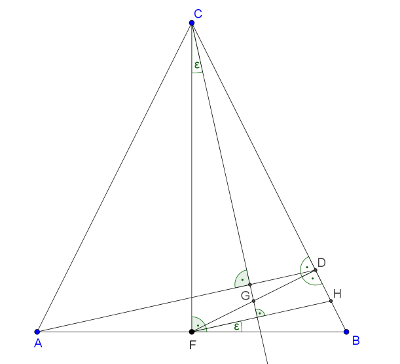
A hasonlóság miatt a két háromszögben a berajzolt súlyvonalak és az átfogók által bezárt szög is megegyezik: \(\displaystyle BFH∡=FCG∡=\varepsilon\).

A szögek egyik szára merőleges egymásra, \(\displaystyle BF⊥FC\), ezért \(\displaystyle FH⊥CG\).

\(\displaystyle FH\) az \(\displaystyle ABD\) háromszög középvonala, hiszen az oldalfelező pontjait köti össze, ezért \(\displaystyle FH‖AD\). Ebből már következik, hogy \(\displaystyle AD⊥CG\).

Statistics:

33 students sent a solution.
5 points:	Agócs Katinka, Édes Lili, Horváth 31 László, Kocsis Júlia, Komoróczy Ádám, Kormányos Hanna Rebeka, Magyar 257 Boglárka, Mészáros Melinda, Nagy Olivér, Németh Csilla Márta, Rittgasszer Ákos, Surján Anett, Szécsi Adél Lilla, Szilágyi Éva, Takács 666 Réka, Tanács Viktória, Tatai Mihály, Thuróczy Mylan, Török Boldizsár, Zsombó István.
4 points:	Kocsis Ábel, Wolff Vilmos.
2 points:	6 students.
0 point:	5 students.

Problems in Mathematics of KöMaL, February 2017