 Problem C. 1407. (March 2017)
Problem C. 1407. (March 2017)
C. 1407. In a parallelogram \(\displaystyle ABCD\), \(\displaystyle M\) and \(\displaystyle N\) are points on sides \(\displaystyle AD\) and \(\displaystyle DC\), respectively, such that \(\displaystyle \frac{AM}{MD}=\frac{DN}{NC}=\frac{7}{11}\). Let \(\displaystyle P\) denote the intersection of lines \(\displaystyle BM\) and \(\displaystyle AN\).
Prove that the areas of triangle \(\displaystyle APB\) and quadrilateral \(\displaystyle DMPN\) are equal.
(Based on the idea of L. Longáver, Nagybánya)
(5 pont)
Deadline expired on April 10, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Használjuk az ábra jelöléseit.
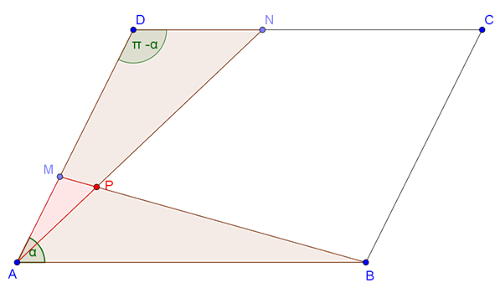
Mivel \(\displaystyle \frac{MD}{AM}=\frac{NC}{DN}=\frac{11}{7}\) és \(\displaystyle AD=AM+MD\) és \(\displaystyle DC=DN+NC\), így \(\displaystyle AD=AM+\frac{11}{7} AM=\frac{18}{7} AM\), valamint \(\displaystyle DC=DN+\frac{11}{7} DN=\frac{18}{7} DN\). Ebből \(\displaystyle AM=\frac{7}{18} AD\) és \(\displaystyle DN=\frac{7}{18} DC\).
\(\displaystyle T_{ABMΔ}=\frac{AB\cdot AM\cdot \sinα}{2}=\frac{7}{18}\cdot\frac{AB\cdot AD\cdot \sinα}{2},\)
\(\displaystyle T_{ADNΔ}=\frac{AD\cdot DN\cdot \sin(π-α)}{2}=\frac{7}{18}\cdot\frac{AD\cdot DC\cdot \sinα}{2}.\)
Mivel a paralelogrammában \(\displaystyle AB=DC\), ezért \(\displaystyle T_{ABMΔ}=T_{ADNΔ}\). Így \(\displaystyle T_{APBΔ}=T_{ABMΔ}-T_{AMPΔ}=T_{ADNΔ}-T_{AMPΔ}=T_{DMPN}\). Tehát \(\displaystyle T_{APBΔ}=T_{DMPN}\).
Statistics:
102 students sent a solution. 5 points: 84 students. 4 points: 5 students. 3 points: 6 students. 2 points: 1 student. 0 point: 5 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, March 2017
