Problem C. 1408. (March 2017)

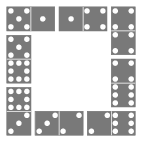
C. 1408. Eight different dominoes are laid on the table, according to the rules of the game, so that they form a closed-up square (the figure shows a possible arrangement). What are the smallest and largest possible values of the sum of the dots on the dominoes?

(5 pont)

Deadline expired on April 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megjegyzés. Legjobb szándékunk ellenére sem lett teljesen egyértelmű a feladat. Mi két készletet ismertünk: a 0-tól 6-ig és a 0-tól 9-ig pöttyözöttet. Az ábrával kizártuk azt a dominókészletet, amiben 0-tól 6-ig szerepelnek a pöttyök, ám van ezeken kívül másmilyen is, amiben ilyen dominók szerepelhetnek. A megoldásból látni lehet, hogy ez csak a maximális értéknél számít, itt elfogadjuk a 6-oson kívül bármelyik létező készletet.

Megoldás. A pontok helyett számokat írunk a dominókra, így egyszerűbb a leírás.

Először keressük meg a legkisebb értéket. Írjuk fel egy táblázatba a dominók legkisebb értékeit:

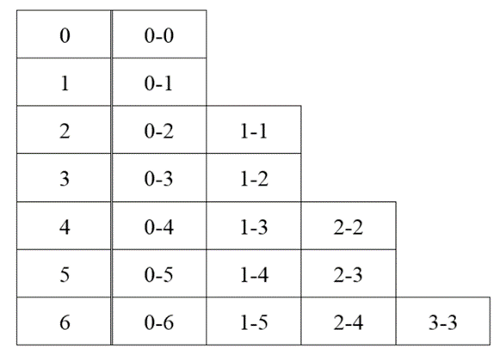
Minden dominó mindkét oldala egy-egy másikkal érintkezik, mindegyiknek van párja, így minden felhasznált szám páros sokszor fordul elő a 8 dominón, azaz 16 oldalon.

Vegyük sorba az eseteket aszerint, hogy hány dominó tartalmaz 0 számot.

a) Ha van 6 olyan dominó, amely tartalmaz 0-t, ezek között nem szerepelhet a 0-0 dominó, mert akkor páratlan lenne a 0-k száma. Így a 0-1, 0-2, 0-3, 0-4, 0-5, 0-6 dominókról van szó. Ekkor a maradék két dominón lévő 4 hely nem elég ahhoz, hogy minden szám kétszer szerepeljen.

b) Ha 5 dominó tartalmaz 0-t, akkor a páros darabszám miatt a 0-0 dominó is köztük van. Az 5 legkisebb ilyen dominó: 0-0, 0-1, 0-2, 0-3, 0-4. Ezekhez biztosan szükséges egy-egy az 1, 2, 3, 4 számokból, ez két dominót jelent. A maradék egy dominó legkisebb lehetséges értéke a táblázat alapján az 1-1.

Tehát ekkor az összeg minimum: \(\displaystyle (1+2+3+4)\cdot2+1+1=22\).

c) Ha 4 dominó tartalmaz 0-t, akkor a páros darabszám miatt a 0-0 nem lehet köztük. Így a legkisebb összeg a 0-1, 0-2, 0-3, 0-4 esetben lesz. Ekkor, hasonlóan az előző esethez, szintén kell még egy-egy az 1, 2, 3, 4-es számokból, két dominón. A maradék két dominó a b) esetben 0-0 és az 1-1 voltak. Itt most a 0-0 nem szerepelhet, így a minimum összeg biztosan nagyobb lesz 22-nél.

d) Ha 3 dominó tartalmaz 0-t, akkor szerepelnie kell a 0-0 dominónak. A 0-0, 0-1, 0-2 választás a legkedvezőbb. Lesz 5 olyan dominó, amin nem szerepel 0. A táblázat alapján a legkisebb összeghez az 1-1, 1-2, 1-3, 2-2 dominók, illetve az 1-4 és 2-3 dominók közül az egyik kellene. Így az összeg 21 lenne.

Azonban, ha az utolsó dominó az 1-4, akkor a nyolc dominó: 0-0, 0-1, 0-2, 1-1, 1-2, 1-3, 2-2, 1-4, és ekkor csak 1 db 4-es és 1 db 3-as van.

Ha az utolsó dominó a 2-3, akkor a nyolc dominó: 0-0, 0-1, 0-2, 1-1, 1-2, 1-3, 2-2, 2-3. Ekkor 5 db 2-es van, ez sem páros, nem lehetséges.

Így legalább egy dominót mindkét esetben ki kell cserélni, aminek következtében az összeg nőni fog, nem lehet 21, minimum 22 lesz.

e) Hat darab, 0-t nem tartalmazó dominóval a legkisebb elérhető összeg a táblázat szerint 23. Így, ha csak 2, 1 vagy 0 db dominó tartalmaz 0 számot, akkor az összeg biztosan nagyobb lesz 22-nél.

Az összes esetre beláttuk, hogy az összeg minimum 22 pötty lehet, erre egy példa:

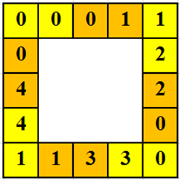
A maximum érték 9 pötty esetén: A maximális érték úgy is kiszámolható, hogy az előző példában minden \(\displaystyle x\) számot kicserélünk (\(\displaystyle 9-x\))-re. Tehát a maximális érték: \(\displaystyle 16\cdot9-22=122\) pötty. Erre egy példa:

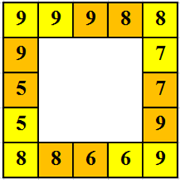
A maximum érték 8 pötty esetén: A maximális érték úgy is kiszámolható, hogy az előző példában minden \(\displaystyle x\) számot kicserélünk (\(\displaystyle 8-x\))-re. Tehát a maximális érték: \(\displaystyle 16\cdot8-22=106\) pötty.

Erre egy példa:

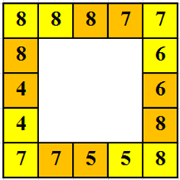
A többi dominókészlet esetén is hasonlóan adható meg a pöttyök számának maximuma.

Vida Tamás (Győr, Kazinczy F. Gimn., 9. évf.) dolgozata alapján

Statistics:

172 students sent a solution.
5 points:	81 students.
4 points:	5 students.
3 points:	5 students.
2 points:	24 students.
1 point:	5 students.
0 point:	43 students.
Unfair, not evaluated:	9 solutionss.

Problems in Mathematics of KöMaL, March 2017