Problem C. 1411. (March 2017)

C. 1411. The angle at vertex \(\displaystyle C\) of a triangle \(\displaystyle ABC\) is \(\displaystyle 120^{\circ}\). \(\displaystyle D\) is the point of side \(\displaystyle AB\) such that \(\displaystyle CD\) is an angle bisector. Show that

\(\displaystyle \frac{1}{CD}=\frac{1}{AC}+\frac{1}{BC}. \)

(D. Fülöp, Pécs)

(5 pont)

Deadline expired on April 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az ábra jelöléseit használva: \(\displaystyle T_{ABCΔ}=T_{ACDΔ}+T_{BCDΔ}\).

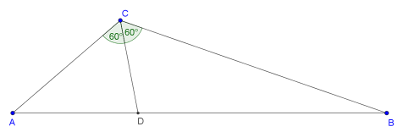
A háromszög trigonometrikus területképletét használva:

\(\displaystyle \frac{AC\cdot BC\cdot\sin120°}{2}=\frac{AC\cdot CD\cdot\sin⁡60°}{2}+\frac{CD\cdot BC\cdot\sin60°}{2}.\)

\(\displaystyle \sin60°=\sin(180°-60°)=\sin⁡120°\). Ezzel leegyszerűsítve és kettővel beszorozva az egyenlet mindkét oldalát:

\(\displaystyle AC\cdot BC= AC\cdot CD+CD\cdot BC.\)

Jobb oldalon CD-t kiemelve:

\(\displaystyle AC\cdot BC= CD\cdot(AC+BC).\)

Mindkét oldalt leosztva a pozitív \(\displaystyle CD\)-vel és \(\displaystyle AC\cdot BC\)-vel:

\(\displaystyle \frac{1}{CD}=\frac{AC+BC}{AC\cdot BC}=\frac{1}{BC}+\frac{1}{AC}.\)

A kívánt egyenletet kaptuk.

Mácz Andrea (Szekszárdi Garay János Gimnázium), 12. évf. dolgozata alapján

Statistics:

49 students sent a solution.
5 points:	Agócs Katinka, Balbisi Mirjam, Demeter Bianka Vivien, Édes Lili, Horváth 31 László, Horváth Dávid, Kassai Levente, Kis 999 Alexandra, Kocsis Ábel, Kocsis Júlia, Mácz Andrea, Magyar 257 Boglárka, Nagy 911 Viktória, Nagy Enikő, Nagy Olivér, Németh Csilla Márta, Pap-Takács Noémi, Pszota Máté, Repovszki Virág, Rittgasszer Ákos, Sántha 001 Balázs, Surján Anett, Szécsi Adél Lilla, Szilágyi Botond, Szilágyi Éva, Takács 666 Réka, Tanács Viktória, Tatai Mihály, Thuróczy Mylan, Török Boldizsár, Ujhelyi Fanni, Varga 274 Tamás, Vezse Botond, Wolff Vilmos, Zeller Doroti, Zsombó István.
4 points:	Ágoston Tamás, Kovács 526 Tamás, Perényi Gellért, Simon Ákos, Szabó Dorottya.
2 points:	1 student.
1 point:	2 students.
0 point:	2 students.
Unfair, not evaluated:	3 solutionss.

Problems in Mathematics of KöMaL, March 2017