Problem C. 1414. (April 2017)

C. 1414. Let \(\displaystyle E\) and \(\displaystyle F\) denote the points that divide side \(\displaystyle CD\) of a unit square \(\displaystyle ABCD\) into three equal parts. Lines \(\displaystyle BE\) and \(\displaystyle BF\) intersect diagonal \(\displaystyle AC\) at \(\displaystyle K\) and \(\displaystyle L\). Find the exact length of \(\displaystyle KL\).

(Matlap, Kolozsvár)

(5 pont)

Deadline expired on May 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Legyen a négyzet oldalhossza \(\displaystyle 3b\) és \(\displaystyle O\) a négyzet átlóinak metszéspontja. Ekkor \(\displaystyle CE=EF=FD=b\). Alkalmazzuk Menelaosz tételét a \(\displaystyle BDE\) háromszögben az \(\displaystyle OK\) szelőre:

\(\displaystyle \frac{OB}{OD}\cdot\frac{KE}{KB}\cdot\frac{CD}{CE}=1.\)

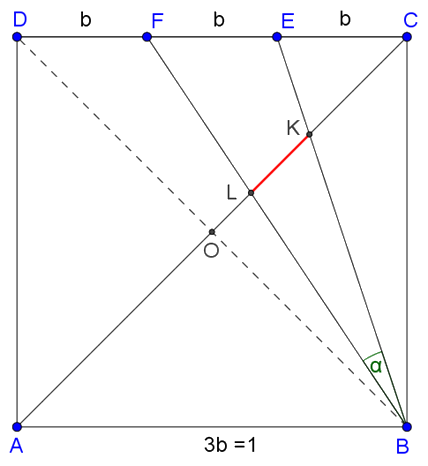
Mivel \(\displaystyle OB=OD\), \(\displaystyle CD=3CE\), így \(\displaystyle \frac{KE}{KB}=\frac13\), tehát a \(\displaystyle K\) pont a \(\displaystyle BE\) szakasz \(\displaystyle E\)-hez közelebbi negyedelő pontja, vagyis \(\displaystyle KB=\frac34 BE\).

A \(\displaystyle BCE\) derékszögű háromszögből \(\displaystyle BE=\sqrt{9b^2+b^2}=b\sqrt{10}\), így \(\displaystyle KB=\frac{3b\sqrt{10}}{4}\).

Hasonlóan a \(\displaystyle BDF\) háromszögben az \(\displaystyle OL\) szelőre alkalmazva Menelaosz tételét: \(\displaystyle \frac{LF}{LB}=\frac23\), tehát az \(\displaystyle L\) pont \(\displaystyle 2:3\) arányban osztja a \(\displaystyle BF\) szakaszt, így \(\displaystyle LB=\frac{3BF}{5}\).

A \(\displaystyle BCF\) derékszögű háromszögből: \(\displaystyle BF=\sqrt{9b^2+4b^2}=b\sqrt{13}\), tehát \(\displaystyle LB=\frac{3b\sqrt{13}}{5}\).

Legyen \(\displaystyle α=KBL∡\), ekkor a \(\displaystyle BEF\) háromszögben a koszinusztételt alkalmazva:

\(\displaystyle EF^2=BE^2+BF^2-2\cdot BE\cdot BF\cdot \cos α,\)

\(\displaystyle \cos α=\frac{BE^2+BF^2-EF^2}{2\cdot BE\cdot BF}=\frac{10b^2+13b^2-b^2}{2b^2 \sqrt{130}}=\frac{11}{\sqrt{130}}.\)

Ezután alkalmazzuk a koszinusztételt a \(\displaystyle BKL\) háromszögben:

\(\displaystyle KL^2=KB^2+LB^2-2\cdot KB\cdot LB\cdot\cos α,\)

\(\displaystyle KL^2=\frac{90b^2}{16}+\frac{117b^2}{25}-2\cdot \frac{3b\sqrt{10}}{4}\cdot\frac{3b\sqrt{13}}{5}\cdot \frac{11}{\sqrt{130}}.\)

Ebből \(\displaystyle KL=\frac{9b\sqrt2}{20}\) adódik, és mivel \(\displaystyle 3b=1\), így \(\displaystyle KL=\frac{3\sqrt2}{20}\).

2. megoldás. Helyezzük a négyzetet koordináta rendszerbe úgy, hogy a csúcsok koordinátái \(\displaystyle A(0;0)\), \(\displaystyle B(1;0)\), \(\displaystyle C(1;1)\) és \(\displaystyle D(0;1)\) legyenek és használjuk a 2. ábra jelöléseit.

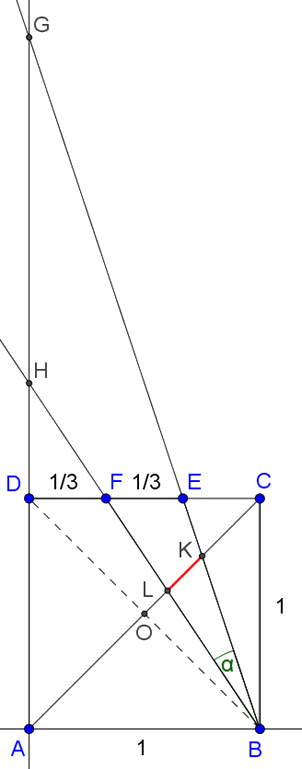
2. ábra

A \(\displaystyle HDF\) és \(\displaystyle HAB\) háromszögek hasonlóságából: \(\displaystyle \frac{HD}{1/3}=\frac{HD+1}{1}\), amiből \(\displaystyle HD=\frac12\), így \(\displaystyle H\left(0; \frac32\right)\).

A \(\displaystyle GDE\) és \(\displaystyle GAB\) háromszögek hasonlóságából: \(\displaystyle \frac{GD}{2/3}=\frac{GD+1}{1}\), amiből \(\displaystyle GD=2\), így \(\displaystyle G(0;3)\).

A \(\displaystyle HB\) egyenes meredeksége \(\displaystyle m=-\frac32\) és az \(\displaystyle y\) tengelyt a \(\displaystyle \frac32\)-nél metszi, így egyenlete: \(\displaystyle y=-\frac32 x+\frac32\).

A \(\displaystyle GB\) egyenes meredeksége \(\displaystyle m=-3\) és az \(\displaystyle y\) tengelyt a 3-nál metszi, így egyenlete: \(\displaystyle y=-3x+3\).

Az \(\displaystyle AC\) egyenes egyenlete: \(\displaystyle y=x\).

A \(\displaystyle K\) pont az \(\displaystyle AC\) és \(\displaystyle GB\) egyenesek metszéspontja:

\(\displaystyle y=x,\)

\(\displaystyle y=-3x+3,\)

amiből \(\displaystyle K\left(\frac34;\frac34\right)\) adódik.

Az \(\displaystyle L\) pont az \(\displaystyle AC\) és \(\displaystyle HB\) egyenesek metszéspontja:

\(\displaystyle y=x,\)

\(\displaystyle y=-\frac32 x+\frac32,\)

amiből \(\displaystyle L\left(\frac35;\frac35\right)\) adódik. Tehát

\(\displaystyle KL=\sqrt{\left(\frac34-\frac35\right)^2+\left(\frac34-\frac35\right)^2}=\left(\frac34-\frac35\right)\sqrt2=\frac{3\sqrt2}{20}.\)

Statistics:

88 students sent a solution.
5 points:	68 students.
4 points:	7 students.
3 points:	3 students.
2 points:	4 students.
1 point:	2 students.
0 point:	4 students.

Problems in Mathematics of KöMaL, April 2017