Problem C. 1419. (April 2017)

C. 1419. In an acute-angled triangle \(\displaystyle ABC\), consider the two circular sectors, each bounded by an arc \(\displaystyle AB\), with one arc passing through the foot of the altitude drawn from \(\displaystyle A\), and the other arc passing through the orthocentre of the triangle. Prove that if \(\displaystyle \angle ACB =45^\circ\) then the areas of the two circular sectors are equal.

(5 pont)

Deadline expired on May 10, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit.

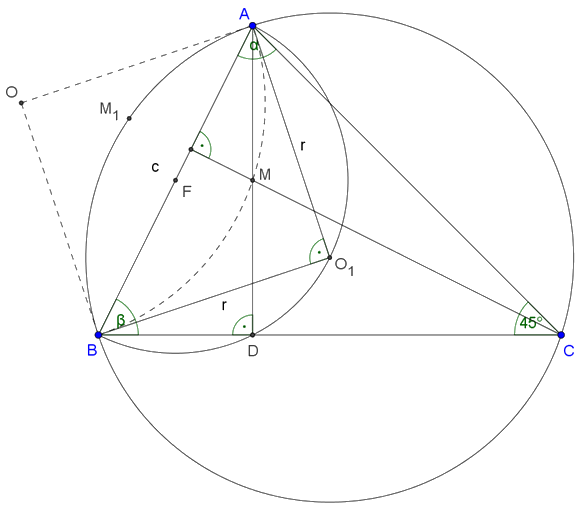
Az \(\displaystyle A\) pontból induló magasság talppontja legyen \(\displaystyle D\). Ekkor \(\displaystyle ADB∡=90°\), így a feladatban szereplő egyik körcikk az \(\displaystyle AB=c\) oldal fölé emelt félkör.

Területe: \(\displaystyle T_1=\frac12\cdot π\cdot\left(\frac c2\right)^2=\frac{c^2}{8} π\).

A másik, \(\displaystyle OAB\) körcikket, melynek íve átmegy a háromszög \(\displaystyle M\) magasságpontján, tükrözzük az \(\displaystyle AB\) oldal egyenesére. Tudjuk, hogy az \(\displaystyle M\) magasságpont \(\displaystyle M_1\) tükörképe rajta van a háromszög körülírt körén, így az \(\displaystyle O\) pont tükörképe \(\displaystyle O_1\), a háromszög körülírt körének középpontja. Mivel az \(\displaystyle ACB∡=45°\) kerületi szög a körben, a hozzá tartozó középponti szög \(\displaystyle AO_1 B∡=90°\). Az \(\displaystyle AO_1 B\) egyenlő szárú derékszögű háromszög átfogója \(\displaystyle AB=c\), így a befogói \(\displaystyle AO_1=BO_1=r=\frac{c}{\sqrt2}\).

Ezért a körcikk területe: \(\displaystyle T_2=\frac14\cdot π\cdot\left(\frac{c}{\sqrt2}\right)^2=\frac{c^2}{8} π\).

Tehát a két körcikk területe megegyezik.

Statistics:

20 students sent a solution.
5 points:	Agócs Katinka, Édes Lili, Kocsis Júlia, Magyar 257 Boglárka, Nagy Olivér, Németh Csilla Márta, Perényi Gellért, Rittgasszer Ákos, Surján Anett, Szalay Gergő, Szilágyi Botond, Szilágyi Éva, Szőnyi Laura, Tanács Viktória, Tatai Mihály, Török Boldizsár, Wolff Vilmos, Zsombó István.
4 points:	Kovács 526 Tamás.
0 point:	1 student.

Problems in Mathematics of KöMaL, April 2017