 Problem C. 1422. (May 2017)
Problem C. 1422. (May 2017)
C. 1422. In a single-storey rectangular apartment, there is at most one door connecting any pair of rooms. In addition, in each room there is at most one exit from the apartment. If the apartment consists of four rooms, what is the maximum possible number of doors altogether?
(5 pont)
Deadline expired on June 12, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Szemléltessük a feladatot egy 5 csúcsú egyszerű gráffal, melynek csúcsai a négy szobát és a külső teret jelentik. Két pont között van él, ha a két térrész között van ajtó. Az 5 csúcsú teljes gráf éleinek száma 10. Tehát maximum 10 ajtó lehetne. De a gráfnak síkba rajzolhatónak kell lenni, mert két szoba között csak akkor lehet ajtó, ha a két szobának van közös fala. Ekkor a két szobának megfelelő két csúcs síkban közvetlenül összeköthető egy éllel. Ha két szobának nincs közös fala, akkor a gráfban a két szobának megfelelő csúcsukat összekötő él metszeni fog egy másik élt. Az ábrán látható példán a \(\displaystyle B\) és \(\displaystyle D\) szoba között nem lehet ajtó, vagyis a \(\displaystyle BD\) élt nem tudjuk síkban meghúzni.
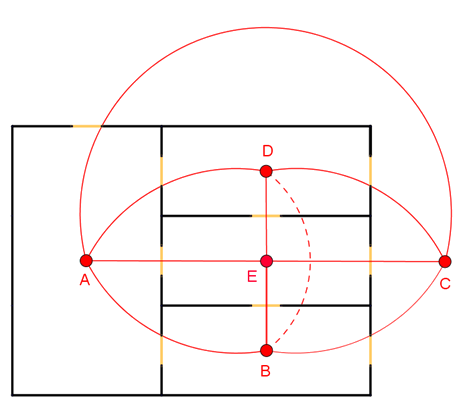
Az öt csúcsú teljes gráfban, ha síkbarajzolható lenne, akkor az Euler-formula szerint 7 tartománynak kellene lennie (most a nagy tartományt is beleszámítjuk). Mivel minden tartományhoz legalább 3 él tartozik, és minden él pontosan két tartományhoz tartozik, ezért az élek számára \(\displaystyle \frac{3\cdot7}{2}\) egy alsó becslést ad, ami ellentmondás, hiszen csak 10 él van. Tehát az 5 csúcsú teljes gráfot nem tudjuk síkbarajzolni. Így a gráfnak csak 9 éle lehet, vagyis legfeljebb 9 ajtó tartozhat a lakáshoz. Ez az ábra szerint meg is valósítható.
Statistics:
125 students sent a solution. 5 points: 51 students. 4 points: 35 students. 3 points: 12 students. 2 points: 8 students. 1 point: 10 students. 0 point: 9 students.
Problems in Mathematics of KöMaL, May 2017
