Problem C. 1425. (May 2017)

C. 1425. Triangle \(\displaystyle ABC\) is right-angled at \(\displaystyle C\), and its Fermat point (see https://en.wikipedia.org/wiki/Fermat_point) is \(\displaystyle I\). Given that \(\displaystyle IC=12\) mm and \(\displaystyle IB=16\) mm, find the length of the line segment \(\displaystyle IA\).

(5 pont)

Deadline expired on June 12, 2017.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Mivel a háromszög derékszögű, így nem lehet \(\displaystyle 120°\)-nál nagyobb szöge, ezért az izogonális pontból mindhárom oldal \(\displaystyle 120°\)-os szögben látszik: \(\displaystyle AIB∡=BIC∡=AIC∡=120°\).

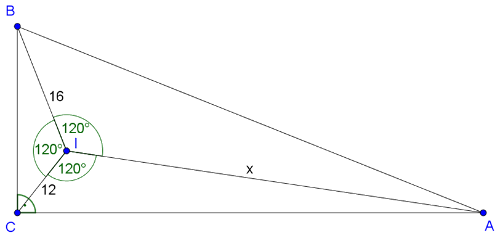
Legyen \(\displaystyle IA=x\). Alkalmazzuk a koszinusz tételt a részháromszögekre, felhasználva, hogy \(\displaystyle \cos 120°=-\frac12\).

\(\displaystyle BC^2=16^2+12^2-2\cdot16\cdot12\cdot-\frac12=592,\)

\(\displaystyle AC^2=12^2+x^2-2\cdot12\cdot x\cdot-\frac12=x^2+12x+144,\)

\(\displaystyle AB^2=16^2+x^2-2\cdot16\cdot x\cdot-\frac12=x^2+16x+256.\)

Alkalmazzuk az ABC háromszögre a Pitagorasz-tételt:

\(\displaystyle AB^2=BC^2+AC^2.\)

A koszinusz tételekből kapott eredményeket behelyettesítve:

\(\displaystyle x^2+16x+256=592+x^2+12x+144.\)

Ezt rendezve \(\displaystyle 4x=480\), amiből \(\displaystyle x=120\). Tehát \(\displaystyle IA=120\) mm hosszú.

Statistics:

22 students sent a solution.
5 points:	Agócs Katinka, Édes Lili, Kocsis Ábel, Kocsis Júlia, Magyar 257 Boglárka, Nagy Olivér, Németh Csilla Márta, Perényi Gellért, Pszota Máté, Rittgasszer Ákos, Sipos Fanni Emma, Surján Anett, Szalay Gergő, Szécsi Adél Lilla, Szilágyi Éva, Szőnyi Laura, Tatai Mihály, Thuróczy Mylan, Wolff Vilmos, Zsombó István.
4 points:	Mácz Andrea.
0 point:	1 student.

Problems in Mathematics of KöMaL, May 2017