Problem C. 801. (March 2005)

C. 801. There is a rectangle inscribed in the pythagorean triangle whose sides are 3, 4, 5 units long, respectively. The vertices of the rectangle are incident to the sides of the triangle and the ratio of its perpendicular sides is 1:3. Determine the dimensions of the rectangle.

(5 pont)

Deadline expired on April 15, 2005.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A téglalapot többféleképpen elhelyezhetjük a háromszögben. Legegyszerűbb eset az, amikor a téglalap oldalai párhuzamosak a háromszög befogóival:

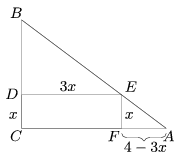
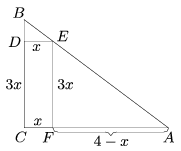
A háromszög csúcsai A, B és C. AC=4, BC=3, AB=5 egység. A téglalap csúcsai C, D, E és F az ábra szerint. Az ABC és AEF derékszögű háromszögek hasonlóságából az első esetben $\frac{4-3x}{4}= \frac{x}{3}$ , és innen 12-9x=4x, $x=\frac{12}{13}$ és $3x=\frac{36}{13}$ .

A második esetben $\frac{4-x}{x}= \frac{3x}{3}$ ; $x=\frac{4}{5}$ és $3x=\frac{12}{5}$ .

A másik lehetőség ez elhelyezésre, amikor a téglalap egyik oldala merőleges az átfogóra:

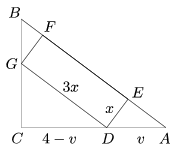
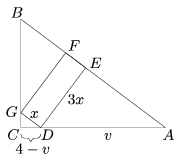
A keletkezett derékszögű háromszögek mind hasonlók egymáshoz, mert megfelelő szögeik egyenlők. Az első esetben: $\frac{v}{x}= \frac{5}{3}$ , $v=\frac{5}{3}\,x$ ; $\frac{4-v}{3x}=\frac{4}{5}$ , $4-v= \frac{12}{5}\,x$ ; ezért $\frac{5}{3}\, x+\frac{12}{5}\, x=4,$ innen $x=\frac{60}{61}, 3x=\frac{180}{61}.$ A második esetben: $\frac{v}{3x}= \frac{5}{3}$ , $v=5\,x$ ; $\frac{4-v}{4}=\frac{x}{5}$ , $4-v= \frac{4}{5}\,x$ ; ezért $5\, x+\frac{4}{5}\, x=4,$ innen $x=\frac{20}{29}, 3x=\frac{60}{29}$ .

Statistics:

225 students sent a solution.

5 points: 87 students.

4 points: 73 students.

3 points: 29 students.

2 points: 24 students.

1 point: 4 students.

0 point: 2 students.

Unfair, not evaluated: 6 solutionss.

Problems in Mathematics of KöMaL, March 2005

225 students sent a solution.
5 points:	87 students.
4 points:	73 students.
3 points:	29 students.
2 points:	24 students.
1 point:	4 students.
0 point:	2 students.
Unfair, not evaluated:	6 solutionss.

Already signed up?
New to KöMaL?