 Problem C. 802. (March 2005)
Problem C. 802. (March 2005)
C. 802. We want to prepare a folding rectangular dining table which when closed is in the position ABCD, when rotated about a pin by ninety degrees is in the position A'B'C'D' and it arrives to the position B1B'C'C1 when unfolded. (See the figure.)
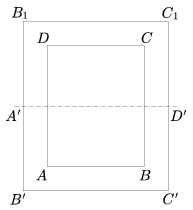
Where shall we put the pin about which the table rotates? How shall we set the dimensions of the table ABCD if, in case of a big fat dinner an even larger table could be produced from the position B1B'C'C1 by repeating the previous procedure, i.e. rotating the table by right angle about the very same pin and unfolding it once more? (Proposed by Papp Zoltán Dániel, Szeged)
(5 pont)
Deadline expired on April 15, 2005.
Sorry, the solution is available only in Hungarian. Google translation
Jelöljük a csapszeg helyét P-vel. Az A pont az első forgatás után az A' pontba megy át, a második után pedig az A'' pontba. Az A' pont éppen az első szétnyitás utáni asztallap élének felezőpontja, így a második forgatás után az A'' pont az ábra középpontjában lesz.
Ugyanakkor a két derékszögű forgatás miatt , vagyis a P pont az AA'' szakasz felezőpontja. De mivel az APA' háromszög és az A'PA'' háromszög egybevágó egyenlőszárú derékszögű háromszögek, ezért az
, vagyis az A' pont éppen az eredeti asztallap AD élének felezőpontja, továbbá AA'=A'A'' miatt AD=AB is teljesül. Tehát az asztallapot négyzetnek kell választanunk, ha kétszer egymás után ugyanazon csapszeg körül szeretnénk végrehajtani a forgatást.
Statistics:
126 students sent a solution. 5 points: Antali Máté, Árvay Anna, Bakacsi Péter, Bitvai Zsolt, Csató Bertalan, Dudás 904 Ádám, Gábor Attila, Gombkötő Tamás, Györök Péter, Gyurcsik Judit, Hauck Zsuzsanna, Juhász 658 Péter, Kiss-Tóth Annamária, Madocsai Judit, Mezei Bálint, Oláh 987 Gábor, Peregi Tamás, Reiter Viktor, Salamon László, Salát Zsófia, Simon Gergely, Szántó Zsolt, Szilágyi Zsombor, Tassy Gergely, Tomanek Ferenc Áron, Tóth Bálint, Varga 111 Péter. 4 points: Blázsik Zoltán, Buday Gáspár, Csörgő 10 Gábor, Dobos Gergely, Elekes Csaba, Germán Olivér, Juhász Zsófia, Kornis Kristóf, Lakatos Dóra, Zöld Péter. 3 points: 22 students. 2 points: 38 students. 1 point: 14 students. 0 point: 15 students.
Problems in Mathematics of KöMaL, March 2005
