 Problem C. 803. (March 2005)
Problem C. 803. (March 2005)
C. 803. Solve the simultaneous equations
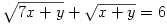
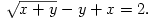
(5 pont)
Deadline expired on April 15, 2005.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Rendezzük az (1) egyenletet, majd emeljük négyzetre:
Innen . A négyzetgyökvonás definíciója értelmében
, azaz x
 6. A
6. A most kapott értékét helyettesítsük be a (2) egyenletbe:
Innen x=2y-2. Helyettesítsünk (2)-be:
Rendezés és négyzetre emelés után a következő másodfokú egyenletet kapjuk:
y2-11y+18=0.
Ebből y1=9 és x1=16; vagy y2=2 és x2=2. A feltétel szerint x 6, emiatt csak az x2=2, y2=2 lehet megoldása az egyenletnek. Helyettesítéssel könnyen ellenőrizhetjük, hogy ez valóban megoldás is.
6, emiatt csak az x2=2, y2=2 lehet megoldása az egyenletnek. Helyettesítéssel könnyen ellenőrizhetjük, hogy ez valóban megoldás is.
Veres Gábor Pál (Miskolc, Földes Ferenc Gimn., 9. évf.)
Statistics:
184 students sent a solution. 5 points: 145 students. 4 points: 8 students. 3 points: 7 students. 2 points: 4 students. 1 point: 8 students. 0 point: 7 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, March 2005
