 Problem C. 807. (April 2005)
Problem C. 807. (April 2005)
C. 807. The lengths of two adjacent sides of a quadrilateral are 2 units and 1 unit, and they enclose an angle of 60o. The quadrilateral is cyclic and it is also a tangent quadrilateral. What are the lengths of the other two sides?
(5 pont)
Deadline expired on May 17, 2005.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen ABCD a keresett négyszög.
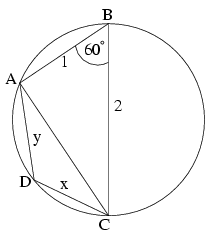
Az ABC háromszögre írjuk fel a koszinusz tételt.
AC2=12+22-2.1.2cos 60o.
Innen AC2=3, és így . Mivel a négyszög húrnégyszög, azért ADC szöge 120o-os. Jelölje az oldalakat AD=y, DC=x. Mivel a négyszög érintőnégyszög is, azért 1+x=2+y és innen y=x-1.
Írjuk fel az ADC háromszögre is a koszinusz tételt: 3=x2+y2+xy, az y=x-1 helyettesítéssel 3=x2+(x-1)2+x(x-1). Innen 3x2-3x-2=0, és így ,
. Tehát csak egy megoldás van: x=1,4574, y=1,4574-1=0,4574.
Statistics:
167 students sent a solution. 5 points: 146 students. 4 points: 2 students. 3 points: 2 students. 2 points: 2 students. 1 point: 9 students. 0 point: 6 students.
Problems in Mathematics of KöMaL, April 2005
