Problem C. 809. (April 2005)

C. 809. The midpoint of the edge AE of the unit cube ABCDEFGH is P, and the midpoint of the face BCGF is R.

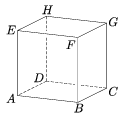
a) Find the area of the intersection of the cube with the plane through the points P, B, R.

b) The above plane cuts the cube into two solids. What is the ratio of the volumes of the two parts?

(5 pont)

Deadline expired on May 17, 2005.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelölje I az EH él felezőpontját. Ekkor $IP \parallel GB$ , tehát a PBR pontokon átmenő sík megegyezik a PBGI pontokon átmenő síkkal.

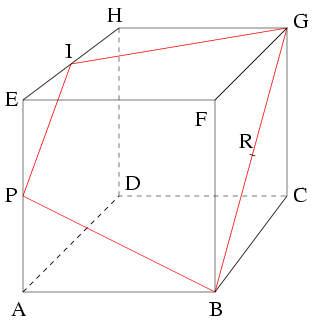
a) A PBGI négyszög trapéz, $BG=\sqrt{1^2+1^2}=\sqrt2$ , $PI=BG/2={\sqrt2\over2}$ , $IG=PB=\sqrt{1^2+0,5^2}={\sqrt5\over2}$ . A trapéz magassága szintén a Pitagorasz-tétel segítségével számolható: $m=\sqrt{PB^2-((BG-PI)/2)^2}=\sqrt{18/16}=\sqrt2\cdot3/4$ . A trapéz területe ezek alapján:

$t={(\sqrt2+\sqrt2/2)\cdot\sqrt2\cdot3/4\over2}=9/8.$

b) BFGIEP csonkagúla. T_BFG=1/2, T_IEP=1/8, a magasság 1, így a csonkagúla térfogata:

$V={1\over3}\cdot\left({1\over2}+\sqrt{{1\over2}\cdot{1\over8}}+{1\over8}\right)={7\over24}.$

A másik rész térfogata $1-{7\over24}={17\over24}$ , így a két rész térfogatának aránya ${7\over17}$ .

Statistics:

172 students sent a solution.

5 points: 99 students.

4 points: 21 students.

3 points: 24 students.

2 points: 13 students.

0 point: 11 students.

Unfair, not evaluated: 4 solutionss.

Problems in Mathematics of KöMaL, April 2005

172 students sent a solution.
5 points:	99 students.
4 points:	21 students.
3 points:	24 students.
2 points:	13 students.
0 point:	11 students.
Unfair, not evaluated:	4 solutionss.

Already signed up?
New to KöMaL?