Problem C. 813. (May 2005)

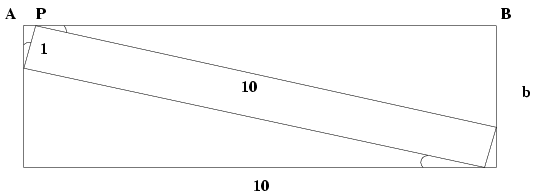
C. 813. One side of a rectangle is 10 cm long. How long is the other side if a 10 cm x1 cm rectangle can be just placed in it in a diagonal position?

(5 pont)

Deadline expired on June 15, 2005.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az ábrán körívvel jelölt egyenlő (hegyes)szögeket jelölje $\alpha$ . Ekkor AP=sin $\alpha$ , PB=10cos $\alpha$ , ezért

10=AP+PB=sin $\alpha$ +10cos $\alpha$ .

A kapott egyenlet mindkét oldalát osszuk el $\sqrt{101}$ -gyel, ekkor

$\frac{10}{\sqrt{101}} = \frac{1}{\sqrt{101}}\sin\alpha + \frac{10}{\sqrt{101}}\cos\alpha .$

Jelölje $\beta$ azt a hegyesszöget, amelyre $\cos\beta = \frac{1}{\sqrt{101}}$ és $\sin\beta = \frac{10}{\sqrt{101}}$ . Így

sin $\beta$ =cos $\beta$ sin $\alpha$ +sin $\beta$ cos $\alpha$ =sin ( $\alpha$ + $\beta$ ).

Mivel 0< $\beta$ < $\alpha$ + $\beta$ < $\pi$ , az egyenlet csak úgy teljesülhet, ha $\beta$ +( $\alpha$ + $\beta$ )= $\pi$ , azaz $\alpha$ = $\pi$ -2 $\beta$ . Ezzel a téglalap másik oldala

b=cos $\alpha$ +10sin $\alpha$ =-cos 2 $\beta$ +10sin 2 $\beta$ =-(2cos² $\beta$ -1)+10^.2sin $\beta$ cos $\beta$ =

$=-(2\frac{1}{101} - 1) + 20 \cdot \frac{10}{\sqrt{101}} \cdot \frac{1}{\sqrt{101}} = \frac{299}{101} \approx 2.96.$

Statistics:

128 students sent a solution.

5 points: 67 students.

4 points: 26 students.

3 points: 13 students.

2 points: 9 students.

1 point: 3 students.

0 point: 10 students.

Problems in Mathematics of KöMaL, May 2005

128 students sent a solution.
5 points:	67 students.
4 points:	26 students.
3 points:	13 students.
2 points:	9 students.
1 point:	3 students.
0 point:	10 students.

Already signed up?
New to KöMaL?