Problem C. 827. (November 2005)

C. 827. You are sitting in an aeroplane. Looking through a window 20 cm from your eye, you can see two boats in the direction of each of the lower corners of the 25 cm×40 cm window, respectively. Given that the plane is flying at an altitude of 10.3 km, and your eye is level with the horizontal bimedian of the window, determine the distance between the two boats.

(5 pont)

Deadline expired on December 15, 2005.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: Készítsünk ábrát!

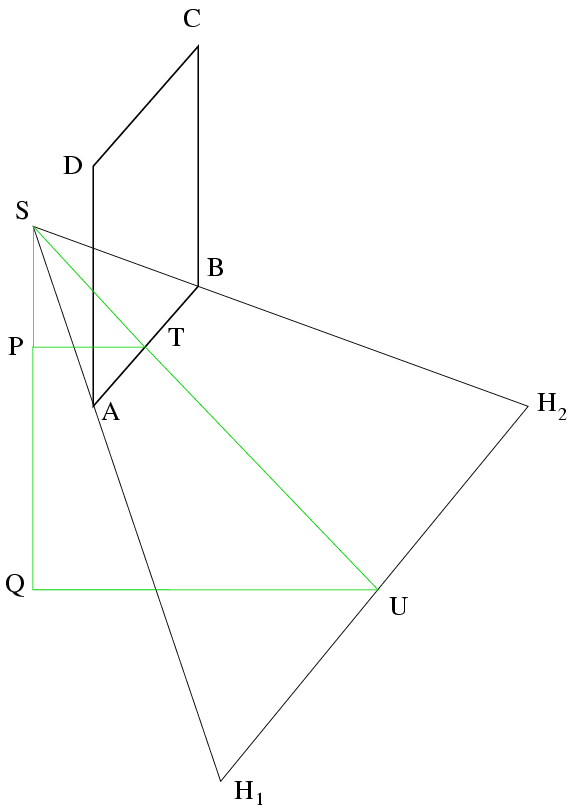
$AB\parallel H_1H_2$ ; $PT\parallel QU$ ; $ST\perp AB$ ; $PT\perp AB$ ; $SP={40\over2}$ cm =20 cm; PT=20 cm; AB=40 cm; SQ=10,3 km.

$SAB_{\triangle}\approx SH_1H_2\triangle$ , így ${H_1H_2\over AB}={SU\over ST}$ , vagyis $H_1H_2={SU\cdot AB\over ST}$ . Mivel $STP_{\triangle}\approx SUQ_{\triangle}$ , ezért ${SU\over ST}={SQ\over SP}$ , ezt az előbbi kifejezésbe beírva, majd a megfelelő értékeket behelyettesítve:

$H_1H_2={SQ\over SP}\cdot AB={10,3{\hbox{\rm~km}}\over{40\over2}{\hbox{\rm~cm}}}\cdot25{\hbox{\rm~cm}}=12,875{\hbox{\rm~km}}.$

Látható, hogy a két hajó távolsága független a szemünk ablaktól való távolságától és vízszintes helyzetétől.

Statistics:

340 students sent a solution.

5 points: 284 students.

4 points: 3 students.

3 points: 7 students.

2 points: 14 students.

1 point: 14 students.

0 point: 16 students.

Unfair, not evaluated: 2 solutionss.

Problems in Mathematics of KöMaL, November 2005

340 students sent a solution.
5 points:	284 students.
4 points:	3 students.
3 points:	7 students.
2 points:	14 students.
1 point:	14 students.
0 point:	16 students.
Unfair, not evaluated:	2 solutionss.

Already signed up?
New to KöMaL?