Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation

Already signed up?
New to KöMaL?

Problem C. 832. (December 2005)

C. 832. Given are the points A(2,1), B(3,4), C(2,11) on the cartesian plane, show that the ray OB bisects the angle AOC.

(5 pont)

Deadline expired on January 16, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás:

OB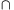 $\cap$ AC=P(2;8/3)

${OC\over OA}={\sqrt{4+121}\over{\sqrt{4+1}}}=5$

${PC\over PA}={25/3\over5/3}=5$

Vagyis ${OC\over OA}={PC\over PA}$ , tehát OP (vagyis OB) az ACO háromszögben az $AOC\measuredangle$ szögfelezője.

Statistics:

362 students sent a solution.

5 points: 350 students.

3 points: 1 student.

2 points: 1 student.

1 point: 4 students.

0 point: 5 students.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, December 2005

362 students sent a solution.
5 points:	350 students.
3 points:	1 student.
2 points:	1 student.
1 point:	4 students.
0 point:	5 students.
Unfair, not evaluated:	1 solutions.