Problem C. 861. (September 2006)

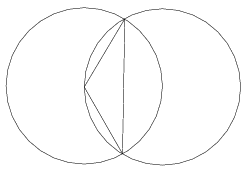
C. 861. In a partial Solar Eclipse, the apparent diameters of the Sun and the Moon were equal. In the time instant when the eclipse was at its maximum, the edge of the Moon's shadow passed through the centre of the Sun's face. What percentage of the Sun's face was eclipsed?

(5 pont)

Deadline expired on October 16, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: A terület két egybevágó körszelet területeként adódik:

$T=2\cdot\left(\frac{r^2\pi}{3}-\frac{r^2\sin120^{\circ}}{2}\right)=r^2\left(\frac{2\pi}{3}-\frac{\sqrt3}{2}\right).$

Így a kérdéses arány:

$\frac{r^2\left(\frac{2\pi}{3}-\frac{\sqrt3}{2}\right)}{r^2\pi}=\frac{2}{3}-\frac{\sqrt3}{2\pi}\approx39,10\%.$

Statistics:

575 students sent a solution.

5 points: 438 students.

4 points: 60 students.

3 points: 36 students.

2 points: 14 students.

1 point: 3 students.

0 point: 16 students.

Unfair, not evaluated: 8 solutionss.

Problems in Mathematics of KöMaL, September 2006

575 students sent a solution.
5 points:	438 students.
4 points:	60 students.
3 points:	36 students.
2 points:	14 students.
1 point:	3 students.
0 point:	16 students.
Unfair, not evaluated:	8 solutionss.

Already signed up?
New to KöMaL?