C. 862. Find the number pairs x, y for which the following inequality is true: 2|x+y||x|+|y|.

(5 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás: A feladatot öt esetre bontjuk.

I. eset: x<0, y<0. Ekkor az egyenlőtlenség így néz ki: 2(-x-y)-x-y, vagyis 0x+y, ami ebben az esetben nem lehetséges.

II. eset: x>0, y>0. Ekkor az egyenlőtlenség így néz ki: 2(x+y)x+y, vagyis x+y0, ami ebben az esetben nem lehetséges.

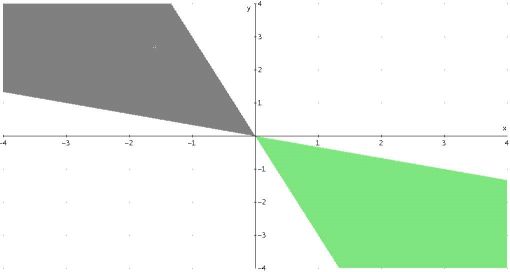
III. eset: x>0, y<0. Ekkor x+y0 esetén azt kapjuk, hogy y-x/3; x+y<0 esetén pedig azt, hogy y-3x. A kettő egyesítve: -3xy-x/3, ami az ábrán a zölddel satírozott rész.

IV. eset: x<0, y>0. Ekkor x+y0 esetén azt kapjuk, hogy y-3x; x+y<0 esetén pedig azt, hogy y-x/3. A kettő egyesítve: -x/3y-3x, ami az ábrán a szürkével satírozott rész.

V. eset: x=0 vagy y=0. Ez csak akkor lehet, ha mindkettő 0, és ez is jó megoldás: x=y=0.

Statistics on problem C. 862. 466 students sent a solution. 5 points: 170 students. 4 points: 58 students. 3 points: 42 students. 2 points: 41 students. 1 point: 57 students. 0 point: 91 students. Unfair, not evaluated: 7 solutions.