Problem C. 867. (October 2006)

C. 867. Starting from the origin in the usual Cartesian coordinate system, a broken line segment is drawn. We arrive back at the y-axis in every fourth step, see the figure.

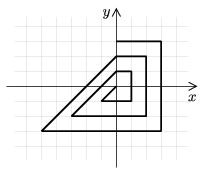
Using a certain ball-pen and a coordinate system with unit length of 0.5 cm, we draw broken line segments of length 8000 meters as in the figure. Count how many times we arrive back at the y-axis.

(5 pont)

Deadline expired on November 15, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

$[(1+3+\ldots+(2n-1))\sqrt2+(5+11+\ldots+(6n-1))]\cdot\frac{1}{2}\leq800\,000,$

$n^2\sqrt2+3n^2+2n\leq1600\,000,$

$(3+\sqrt2)n^2+2n\leq1\,600\,000.$

Másodfokú egyenlőtlenség megoldása nélkül is kitalálható, hogy melyik a legnagyobb n egész szám, amire teljesül: n=601.

Statistics:

459 students sent a solution.

5 points: 235 students.

4 points: 21 students.

3 points: 19 students.

2 points: 27 students.

1 point: 72 students.

0 point: 66 students.

Unfair, not evaluated: 19 solutionss.

Problems in Mathematics of KöMaL, October 2006

459 students sent a solution.
5 points:	235 students.
4 points:	21 students.
3 points:	19 students.
2 points:	27 students.
1 point:	72 students.
0 point:	66 students.
Unfair, not evaluated:	19 solutionss.

Already signed up?
New to KöMaL?