A C. 867. feladat

Rendelje meg a KöMaL-t!

ELTE

VersenyVizsga portál

Kísérletek.hu

Matematika oktatási portál

C. 867. A derékszögű koordinátarendszer origójából indulva rajzolunk egy töröttvonalat az ábra szerint. Minden negyedik szakasz megrajzolása után visszajutunk az y tengelyhez, ahogyan az ábra mutatja.

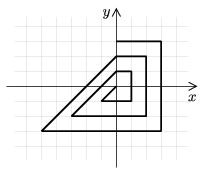
Egy hazánkban gyártott golyóstoll csomagolásáról megtudtuk, hogy az íráshossza 8000 méter. Ha ezzel a tollal megrajzolnánk egy 0,5 cm egységű koordinátarendszerben a megadott 8000 méter hosszúságú vonalat, hányszor érkeznénk vissza az y tengelyhez?

(5 pont)

A beküldési határidő LEJÁRT.

Megoldás.

$[(1+3+\ldots+(2n-1))\sqrt2+(5+11+\ldots+(6n-1))]\cdot\frac{1}{2}\leq800\,000,$

$n^2\sqrt2+3n^2+2n\leq1600\,000,$

$(3+\sqrt2)n^2+2n\leq1\,600\,000.$

Másodfokú egyenlőtlenség megoldása nélkül is kitalálható, hogy melyik a legnagyobb n egész szám, amire teljesül: n=601.

A C. 867. feladat statisztikája

459 dolgozat érkezett.

5 pontot kapott: 235 versenyző.

4 pontot kapott: 21 versenyző.

3 pontot kapott: 19 versenyző.

2 pontot kapott: 27 versenyző.

1 pontot kapott: 72 versenyző.

0 pontot kapott: 66 versenyző.

Nem versenyszerű: 19 dolgozat.

A KöMaL 2006. októberi matematika feladatai

Támogatóink:

ELTE