Problem C. 869. (October 2006)

C. 869. A cylinder of height $\frac{4}{3} R$ is inscribed into a sphere of radius R. Determine the ratio of their volumes.

(5 pont)

Deadline expired on November 15, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelöljük R-rel a gömb, r-rel a henger sugarát, és m-mel a henger magasságát.

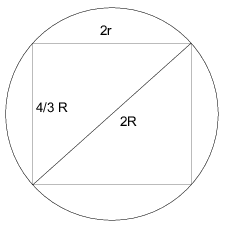
Ekkor az ábra alapján a Pitagorasz-tételt felírva:

$(2R)^2 = (2r)^2 + (\frac43R)^2,$

ahonnan

$r^2 = \frac59R^2.$

A térfogatok aránya innen

$\frac{V_{\rm{henger}}}{V_{\rm{g\"omb}}} = \frac{r^2 \pi m}{\frac{4R^3 \pi}3} = \frac{\frac{5R^2 \pi}9 \cdot \frac43R}{\frac{4R^3 \pi}3} = \frac59.$

Tehát a henger a gömb térfogatának $\frac59$ -része.

Statistics:

570 students sent a solution.

5 points: 451 students.

4 points: 53 students.

3 points: 18 students.

2 points: 23 students.

1 point: 6 students.

0 point: 11 students.

Unfair, not evaluated: 8 solutionss.

Problems in Mathematics of KöMaL, October 2006

570 students sent a solution.
5 points:	451 students.
4 points:	53 students.
3 points:	18 students.
2 points:	23 students.
1 point:	6 students.
0 point:	11 students.
Unfair, not evaluated:	8 solutionss.

Already signed up?
New to KöMaL?