Problem C. 872. (November 2006)

C. 872. Consider a quadrant of a disc of radius 12 cm. A semicircle is drawn over one of the radii bounding the quadrant, and cut out of it. What is the radius of the largest possible circle that can be inscribed in the remaining figure?

(5 pont)

Deadline expired on December 15, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A PQR derékszögű háromszögben RQ²=r²+x², a POR derékszögű háromszögben RO²=6²+x². Az OQR derékszögű háromszögben RQ²+RO²=QO², vagyis r²+x²+6²+x²=(r+6)², amiből 2x²=12r.

ST=SQ+QT, vagyis $12=r+\sqrt{(2x)^2+r^2}=r+\sqrt{24r+r^2}$ , amit rendezve $12-r=\sqrt{24r+r^2}$ , négyzetre emelve és rendezve r=3.

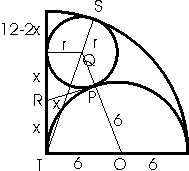
Statistics:

393 students sent a solution.

5 points: 319 students.

4 points: 12 students.

3 points: 5 students.

2 points: 3 students.

1 point: 3 students.

0 point: 51 students.

Problems in Mathematics of KöMaL, November 2006

393 students sent a solution.
5 points:	319 students.
4 points:	12 students.
3 points:	5 students.
2 points:	3 students.
1 point:	3 students.
0 point:	51 students.

Already signed up?
New to KöMaL?